Математическое описание алгоритма вычисления CRC

Алгоритм вычисления CRC основывается на свойствах деления по модулю 2 с остатком двоичных многочленов. Значение CRC являет собой суть, остаток от деления многочлена, соответствующего входному массиву данных, на некоторый постоянный так называемый порождающий многочлен.

Каждой конечной последовательности битов 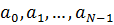взаимно однозначно соответствует двоичный полином [1] 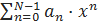его коэффициенты представляют собой исходную последовательность. К примеру, последовательности бит 1011010 соответствует многочлен:

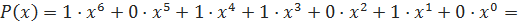
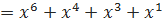
Значение контрольной суммы в алгоритме с порождающим многочленом G(x) степени N определяется, как последовательность бит длиной N, представляющая многочлен R(x), получившийся в остатке от деления многочлена P(x), представляющего входящий массив бит, на порождающий многочлен G(x):

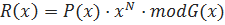
Где

R(x) – многочлен, представляющий значение CRC;

P(x) – многочлен, коэффициенты которого представляют входные данные;

G(x) – порождающий многочлен;

N – степень порождающего многочлена.

При делении с остатком исходного многочлена (представляющего входной массив бит) на порождающий многочлен G(x) степени N можно получить 2^N различных остатков от деления. Многочлен G(x) как часто бывает является неприводимым. Порождающий многочлен подбирают обычно в соответствии с требованиями к хэш-функции в для каждого конкретного применения.

Однако следует отметить, что существует множество стандартизованных образующих полиномов, имеющих хорошие математические и корреляционные свойства (минимальное число коллизий, простота вычисления) в таблице 2 перечислены некоторые стандартные порождающие полиномы.

Дата добавления: 2015-08-31