Зрівноваження мережі та оцінка точності отриманих результатів 1 страница

Побудова схеми та укрупненої схеми мережі полігонометричних ходів за вихідними пунктами

Розділ 4. ЗРІВНОВАЖЕННЯ МЕРЕЖІ ПОЛІГОНОМЕТРИЧНИХ ХОДІВ

Схему мережі полігонометричних ходів будуємо так:

Складаємо саму схему, де підписуємо назви (номери) всіх пунктів (точок), а також номери ходів. У вузлах відображаємо напрями. Виписуємо виміряні кути (позначаються дугами) та довжини ліній (горизонтальні прокладення).

На укрупненій схемі мережі вказуємо назви вихідних та вузлових пунктів та напрямів. В стовпчик записуємо такі дані: номер ходу, суму виміряних приростів, нев’язки, довжину ходу, кількість ходів.

У способі послідовних наближень використовуємо лише укрупнену схему полігонометричних ходів 4 класу.

Роздільне зрівноваження мережі полігонометричних ходів можна проводити: способом еквівалентної заміни, способам послідовних наближень (вузлів), способом полігонів В.В. Попова. Цими способами спочатку отримують дирекційні кути вузлових напрямків і координати вузлових пунктів, а потім, використовуючи їх як вихідні, зрівноважують окремі ходи також нестрогим способом, розподіляючи нев’язки в прирости координат прямо пропорційно до числа лінії або до довжин ліній.

В курсовій роботі мережу полігонометричних ходів будемо зрівноважувати способом послідовних наближень. Спочатку складаємо укрупнену схему мережі полігонометричних ходів 4 класу (рис. 5.1).

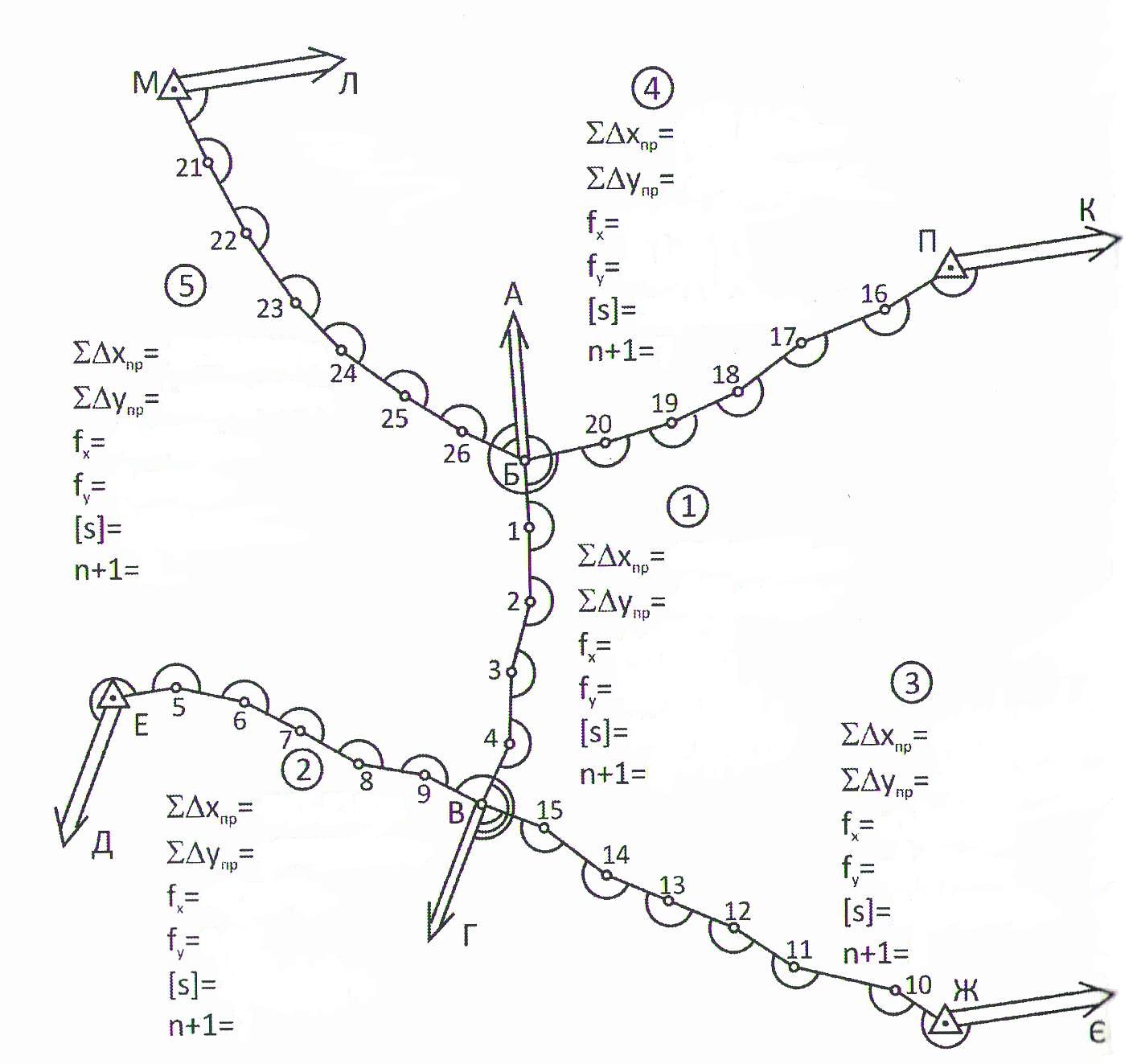
Рис. 4.1 Укрупнена схема мережі полігономертичних ходів 4 класу

Обчислення починаємо із розрахунку дирекційних кутів вихідних напрямків. За координатами вихідних пунктів знаходимо румби:

r = arctg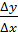

Дирекційні кути напрямку КП вираховуємо за румбом з врахуванням чверті, в якій він знаходиться, а чверть визначаємо за знаками приростів координат (ΔХ; ΔY). Формули для вирахування дирекційних кутів за румбами наведені в (таблиці 4.1).

Таблиця 4.1 – Знаходження дирекційного кута за румбами

№ чверті	Знаки приростів	Формули
І		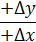α = r
ІІ		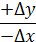α = 180˚- | r |
ІІІ		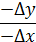α = 180˚+ r
ІV		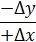α = 360˚- | r |

Далі вираховуємо суми кутів в кожному ході. Далі способом послідовних наближень зрівноважуємо дирекційні кути вузлових напрямків Б-А та В-Г (таб. 5.2) в наступній послідовності. Спочатку заповнюємо графи 1-6 таблиці 5.2. Далі вираховуємо вагу кожного ходу за формулою:

p_α= 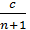і записуємо в графу 7. Значення дирекційного кута вузлового напрямку

Б-А отримуємо двічі з ходів 4 та 5, використовуючи формулу:

α_к= α_п+Σβ_л -180˚(n+1)

Ця формула справедлива для лівих виміряних кутів. Перше наближення дирекційного кута Б-А отримуємо як середнє вагове із значень, вирахуваних з ходів 4 та 5.

Перше наближення дирекційного кута В-Г отримуємо як середнє вагове із значень, вирахованих з ходів 1, 2, 3. Для вирахування дирекційного кута В-Г з ходу 1 використовується не кут Б-А, отриманий в першому наближенні, а зворотний йому А-Б.

Після виконання першого наближення переходимо до другого, дирекційні кути вузлових напрямків обчислюємо в тій самій послідовності. Друге наближення дирекційного кута Б-А отримуємо вже як середнє вагове із значень, вирахуваних із ходів 1, 4, 5. При вирахуванні в другому та наступних наближеннях дирекційного кута Б-А з ходу 1, напрямок ходу змінюється на протилежний, отже виміряні кути β будуть правими і дирекційний кут беде вираховуватись за формулою:

α_к= α_п-Σβ_п +180˚(n+1)

Крім цього, вирахуваний в попередньому наближенні дирекційний кут В-Г змінюємо на зворотній Г-В. обчислення закінчено, коли значення в останніх наближень не будуть відрізнятись між собою (в цілих секундах).

Далі визначаємо поправки υ_βі на кожен хід як різницю між кінцевим значенням і отриманим з і-го ходу в останньому наближенні.

υ_βі =α - α'

Отримавши зрівноважені значення дирекційних кутів вузлових напрямків переходимо до зрівноваження координат вузлових точок. Для цього знаходимо практичні суми приростів ходів, які вираховуємо у відомості вирахування полігонометричних ходів (таб. 5.5). Зрівноваження координат вузлових точок теж виконуємо способом послідовних наближень окремо для абсцис та ординат. Зрівноваження виконуємо у такому порядку:

Заповнюємо графи 1-6 таблиць 4.3, 4.4. Далі вираховуємо ваги суми приростів для кожного ходу за формлою:

p_x = p_y =

Значення абсциси та ординати вузлової точки Б в першому наближенні вираховуємо з ходів 4 і 5 за формулами:

X_к= X_п +ΣΔx

Y_к= Y_п +ΣΔy

Значення координат вузлової точки В в першому наближенні вираховуємо з ходів 1, 2 та 3, використовуючи для першого ходу абсциси та ординати точки Б, отримані в першому наближенні.

Далі переходимо до другого наближення, вираховуючи абсциси і ординати вузлових точок в тій самій послідовності. За вихідні при кожному наступному вирахуванні приймають значення координат, отриманих з попередніх наближень. Закінчують вирахування тоді, коли значення двох останніх наближень не будуть відрізнятись між собою (в міліметрах).

Далі вираховуємо поправки υ_х та υ_у на кожен хід як різницю між кінцевим значенням і отриманих по ходу в останньому наближенні.

υ_х = X - X'_i

υ_у = Y - Y'_i

Отримавши зрівноважені значення координат вузлових точок записуємо їх у відомості вирахування координат точок полігонометричних ходів (таб. 4.5). Далі знаходимо теоритичну суму приростів, вираховуємо нев’язки то вводимо поправки у виміряні прирости. Отримуємо виправлені прирости і розраховуємо координати усіх точок полігонометричних ходів. Всі розрахунки наведені в таблиці 4.5.

Далі виконуємо оцінку точності польових вимірів та зрівноважених значень дирекційних кутів вузлових напрямків та оцінку точності координат вузлових точок.

У відомостях обчислення координат я обчислив дирекційні кути напрямків та за приростами координат розрахував координати точок ходу.

Обчислення дирекційних кутів вузлових напрямків БА та ВГ я виконала способом послідовних наближень. Аналогічно я обчислював значення абсцис та ординат вузлових точок.

Відомість вирахування координат точок полігонометричних ходів 4 класу
№	Виміряні кути β	Виправлені кути β	Дирекційні кути α	Довжини ліній S, м	Прирости координат, м	Координати, м
Виміряні	Виправлені
∆Χ	∆Υ	∆Χ	∆Υ	Χ	Υ
Хід 1
А	°	′	″	°	′	″	°	′	″
			1,3
Б	158	44	43,0	158	44	44,3					2	3			13137,961	14849,776
			1,3				170	41	52,3	482,462	89,801	458,400	89,802	458,402
	195	04	4,0	195	04	5,3					2	3			13227,763	15308,178
			1,3				185	45	57,6	469,957	78,849	471,274	78,850	471,277
	173	34	53,0	173	34	54,3					2	3			13306,613	15779,455
			1,4				179	20	51,9	477,619	-55,366	459,382	-55,364	459,384
	195	14	40	195	14	41,4					2	2			13251,249	16238,839
			1,4				194	35	33,3	420,758	40,307	412,920	40,309	412,923
	197	54	19,0	197	54	20,4					2	2			13291,558	16651,762
			1,3				212	29	50,7	418,618	-66,584	391,526	-66,583	391,528
В	177	27	9,0	177	27	10,3									13224,975	17043,290
Г
	1098	02	48		P = [S] =	2269,414	м		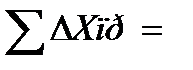87,006	м		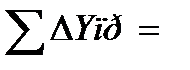	2193,502	м
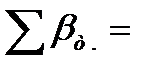
	1098	2	58,11								87,015	м		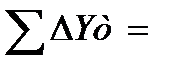	2193,514	м
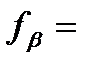+	0	0	7,89		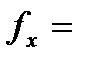						-0,008	м			-0,012	м
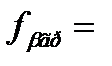±	0	0	12,25		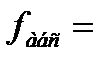						0,015	м
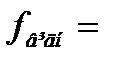
												1/150400

	Відомість вирахування координат точок полігонометричних ходів 4 класу
	№	Виміряні кути β	Виправлені кути β	Дирекційні кути α	Довжини ліній S, м	Прирости координат, м	Координати, м
	Виміряні	Виправлені
	∆Χ	∆Υ	∆Χ	∆Υ	Χ	Υ
	Хід 2
	Д	°	′	″	°	′	″	°	′	″
				1
	Е	207	57	16,0	207	57	18,3					-2	6			10762,730	16775,599
				3				266	11	8,3	413,056	394,836	-132,403	394,834	-132,397
		196	16	0,0	196	16	2,3					-2	7			11157,564	16643,202
				1				282	27	10,6	446,236	451,073	18,135	451,071	18,142
		198	15	51,0	198	15	53,3					-2	6			11608,634	16661,344
				3				300	43	3,9	412,821	387,769	119,755	387,767	119,761
		174	47	49,0	174	47	51,3					-2	6			11996,402	16781,105
				3				295	30	55,2	431,886	402,910	143,063	402,908	143,069
		166	16	13,0	166	16	15,3					-2	6			12399,310	16924,174
				3				281	47	10,4	412,875	432,936	-2,234	432,934	-2,227
		188	31	14,0	188	31	16,3					-2	6			12832,244	16921,947
				2				290	18	26,7	406,933	392,733	121,337	392,732	121,343
	В	279	41	40,0	279	41	42,2									13224,976	17043,290
	Г
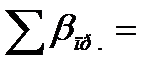
		1411	46	3,0		P = [S] =	2523,807	м		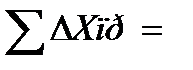2462,257	м			267,653	м
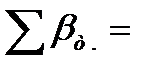
		1411	46	8,6								2462,246	м		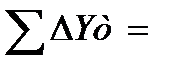	267,691	м
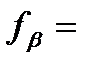	-	0	0	5,60		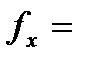						0,011	м			-0,037	м
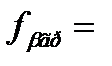	±	0	0	13,23								0,039	м
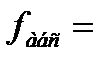
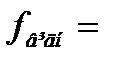
														1/65200
Відомість вирахування координат точок полігонометричних ходів 4 класу
№	Виміряні кути β	Виправлені кути β	Дирекційні кути α	Довжини ліній S, м	Прирости координат, м	Координати, м
Виміряні	Виправлені
∆Χ	∆Υ	∆Χ	∆Υ	Χ	Υ
Хід 3
Є	°	′	″	°	′	″	°	′	″
			0,5						44,3
Ж	199	17	55,0	199	17	54,5					0	-9			16347,946	17878,990
			0,5				197	11	38,8	485,963	-462,852	-143,224	-462,852	-143,234
	172	56	20,0	172	56	1,5					0	-10			15885,094	17735,756
			0,5				183	8	40,3	497,631	-507,246	-27,867	-507,246	-27,877
	192	14	29,0	192	14	30,5					0	-9			15377,849	17707,880
			0,5				205	5	10,8	471,668	-428,865	-200,770	-428,864	-200,779
	174	57	59,0	174	57	27,5					0	-9			14948,984	17507,101
			0,5				194	36	38,4	473,704	-458,595	-119,546	-458,595	-119,555
	177	47	55,0	177	47	1,5					0	-9			14490,389	17387,545
			0,5				190	37	39,9	453,761	-467,270	-87,681	-467,269	-87,690
	191	11	38,0	191	11	52,5					0	-8			14023,120	17299,855
			0,5				205	20	32,4	468,907	-366,006	-173,341	-366,006	-173,349
	166	48	26,0	166	48	23,5					0	-8			13657,113	17126,506
			0,5				190	53	55,9	394,113	-432,138	-83,208	-432,138	-83,216
В	99	18	9,0	99	18	2,5									13224,976	17043,290
Г
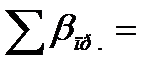
	1374	32	10,00		P = [S] =	3245,747	м		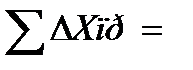-3122,972	м			-835,638	м
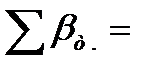
	1374	32	14,12								-3122,970	м		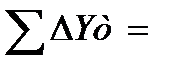	-835,700	м
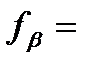+	0	0	4,12		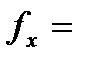						-0,002	м			0,062	м
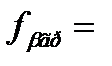±	0	0	14,14								0,062	м
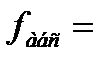
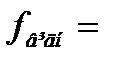
													1/52500

Дата добавления: 2015-08-31