Грубые погрешности и промахи

Более точную оценку значения измеряемой величины можно получить лишь путем ее многократных измерений и соответствующей обработки результатов.

· Источниками промахов нередко бывают ошибки, допу­щенные оператором при измерении. Наиболее характерны­ми из них являются:

· неправильный отсчет по шкале измерительного уст­ройства;

· неправильная запись результата наблюдения (описка), неправильная запись значений отдельных мер использо­ванного набора и т.п.;

· ошибки при манипуляциях с приборами, если они по­вторяются при измерениях;

· внезапные и кратковременные изменения условий измерения;

· незамеченные неисправности средства измерений и др.

Обнаружение и исключение грубых погрешностей

Наличие грубых погрешностей в результатах измерения решается методами математической статистики — статис­тической проверкой гипотез.

Суть метода сводится к следующему: выдвигается нуле­вая гипотеза относительно результата измерения, который вызывает сомнение и рассматривается как промах в связи с большим отклонением от других результатов измерения. При этом нулевая гипотеза заключается в утверждении, что «промах» в действительности принадлежит к изучаемой со­вокупности полученных в данных условиях результатов из­мерений, а получение такого результата — вероятно.

Пользуясь статистическими критериями, необходимо опровергнуть нулевую гипотезу, т.е. доказать ее практическую невероятность. Если это удается, то промах исключают, если нет — то результат измерения оставляют.

Выбор того или иного критерия зависит от многих фак­торов, например, от количества измерений.

Для применения выбранного критерия необходимо сле­дующее.

1. Задаться достаточно малой вероятностью q того, что сомнительный[1] результат действительно мог бы иметь место. Вероятность q называется уровнем значимости и обыч­но выбирается из ряда: 0,10; 0,05; 0,01 и т.д.

2. Определить для данного q критическую область значе­ний критерия проверки нулевой гипотезы.

3. Сравнить фактическое значение критерия с его крити­ческим значением. Если значение критерия попадает в кри­тическую область, то гипотеза отвергается.

Критерии грубых погрешностей

Известно много различных критериев, которые позволя­ют исключить грубые промахи. К ним, в частности, можно отнести критерий 3s, Граббса —Смирнова, Шарлье, Шовенэ, Диксона и др. Эти критерии основаны на статистических оценках параметров распределения, так как в большинстве случаев действительные значения параметров распределе­ния неизвестны.

Критерий 3s

Критерий 3s применяется для результатов измерений, распределенных по нормальному закону. По этому крите­рию считается, что результат, возникающий с вероятностью Р = 0,0027, маловероятен, и его можно считать промахом, если

(4.92)

(4.93)

где

(4.94)

(4.95)

— среднее арифметическое результатов измерения; s — среднее квадратичное отклонение.

Данный критерий дает достаточно надежные результаты только при

п > 30.

Критерий Шарлье

Критерий Шарлье применяют лишь для рядов, количе­ство измерений в которых п > 20. Если количество результатов измерений п > 20, то по теореме Бернулли число ре­зультатов, превышающих по абсолютному значению , будет равно п[1 - Ф(К_Ш)], где Ф(К_Ш) – значение нормиро­ванной функции Лапласа для Z = К_Ш.

Если сомнительным в ряду наблюдений является один результат, то

п[ 1 - Ф(К_Ш)] = 1. (4.96)

Отсюда Ф(К_Ш) =

Критические значения критерия Шарлье можно опреде­лить по табл. 4.4 или вычислить по формуле

(4.97)

(для 5 ≤ п ≤ 100, Р = 0,95).

Таблица 4.4

Критические значения критерия Шарлье

n
КШ	1,30	1,65	1,96	2,13	2,24	2,32	2,58

Пользуясь критерием Шарлье, отбрасывают результат, значение которого превосходит по модулю .

Порядок обнаружения и исключения грубых погрешно­стей и промахов с использованием критерия Шарлье сво­дится к следующему:

· определяется среднее значение результатов измерения

· определяется оценка среднего квадратичного отклоне­ния s(х) по формуле

· определяется расчетное (критическое) значение кри­терия Шарлье по уравнению (4.97);

· определяется абсолютное значение разности сомни­тельного результата, т.е. |х_сомн ^- |;

· сравниваются значения |х_сомн 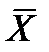^- | и s(х)К_Ш: если х_сомн 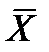^- | > s(х)К_Ш то результат отбрасывают как содержа­щий грубую погрешность; если

|х_сомн 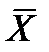^- | < s(х)К_Ш, то ре­зультат не содержит грубой ошибки.

Правило Томпсона

В правиле Томпсона используется статистика

(4.98)

где

— выборочное среднее значение;

— выборочное среднеквадратичное отклонение.

Согласно правилу Томпсона из ряда измерений следует исключать все те результаты измерения х_i, для которых |t_i|>z_m,α при т = п-2.

Критическое значение критерия можно определить по формуле

где x=ln n, y = α (α=0,01;0,05;0,1), 1 ≤ n ≤ 100.

Критерий Граббса — Смирнова

В критерии Граббса —Смирнова используется статистика

(4.100)

где х_с — результат измерения, вызывающий сомнение; X — среднее арифметическое значение ряда измерений; s_x — сред­нее квадратичное отклонение результатов измерения.

Критическая область значений этого критерия опреде­ляется как

P(К_Г>Z_q)=q (4.101)

Значение Кг(q, п) для случая нормального закона рас­пределения результатов измерения в зависимости от уров­ня значимости у и количества наблюдений можно выбрать по табл. 4.5.

Можно вычислить К_Г по формулам

(4.102)

Таблица 4.5

Критерий Граббса-Смирнова

n	КГ(0,1,n)	КГ(0,05,n)	КГ(0,025,n)	КГ(0,01,n)
3,00	1,41	1,41	1,41	1,41
5,00	1,79	1,87	1,92	1,96
10,0	2,15	2,29	2,41	2,54
20,0	2,45	2,62	2,78	2,96
25,0	2,54	2,72	2,88	3,07

К_Г(0,05,n)= 1,2088 - 0,0033л + 0,4965 (4.103)

К_Г(0,025,n) - 1,0158 - 0,0107л + 0,6631 (4.104)

К_Г(0,01,n) - 1,7191 - 0,0197л + 0,8829 (4.105)

(формулы справедливы для 3 ≤ п ≤ 25).

Если при выбранном уровне значимости q и числе на­блюдений п критерий К_Г > К_Г(q, п), то результат отбрасыва­ют как содержащий грубую погрешность.

Порядок обнаружения и исключения грубых погрешно­стей и промахов с использованием критерия Граббса—Смир­нова сводится к следующему:

· определяется среднее значение результатов измерения

· определяется оценка среднего квадратичного отклоне­ния s(x) по формуле

· принимается желаемый уровень значимости из ряда: 0,01; 0,025; 0,05; 0,1;

· определяется расчетное (критическое) значение кри­терия Граббса — Смирнова К_Г(q,n) по одному из уравнений (4.102)—(4.105) для принятого уровня значимости q;

· определяется критерий Граббса —Смирнова по фор­муле (4.100)

· сравниваются значения К_Г и К_Г(q,n):

если К_Г > К_Г(q,n), то результат отбрасывают как содер­жащий грубую погрешность;

если К_Г < К_Г(q,n), то результат не содержит грубой ошибки с принятой вероятностью Р = 1 – q.

Критерий Шовенэ

Критерий Шовенэ основан на тех же предпосылках, что и критерий Шарлье. Его можно использовать если количе­ство результатов измерения меньше 20.

Критическая область для этого критерия определяется неравенством

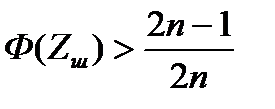(4.106)

Из полученного ряда измерений, содержащего п членов, отбрасывают сомнительный результат — х_k.

Вычисляют среднее арифметическое значение и среднее квадратичное отклонение по формулам

Определяют статистику Z

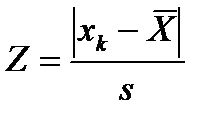(4.107)

Таблица 4.6

Значения M и Z

Z	M	Z	M	Z	M
1,0-1,28		2,06-2,08		2,32
1,3-1,46		2,1		2,34
1,48-1,58		2,12		2,36
1,60-1,68		2,14-2,16		2,38
1,70-1,760		2,18		2,4
1,78-1,82		2,2		2,42
1,84-1,88		2,22		2,44
1,90-1,92		2,24		2,46
1,94-1,98		2,26		2,48
2,00		2,28		2,5
2,02-2,04		2,3		2,52

Вычисляется ожидаемое число отсчетов М, среди кото­рых будет хотя бы один аномальный (промах).

Если М > п, то отсчет х_к считается промахом.

Значения М и Z приведены в табл. 4.6.

При значениях Z ≥ 2,2 значения М можно определить также но формуле

М = int[ехр(0,7639 + 0.2968Z^2,5)].

Критерий Диксона

Критерий Диксона (Кд) — удобный и достаточно мощ­ный критерий. Для использования критерия Диксона ре­зультаты измерений располагают в вариационный возрас­тающий ряд x₁<x₂<…<x_n.

Критерий Диксона определяется по формуле

К_д (4.108)

Критическая область для этого критерия

P(К_д>Z_д(q,n))= q (4.109)

Значения К_д(q,n) вычисляются по таблице 4.7.

Таблица 4.7

Критические значения критерия Диксона

n	КД(0,1,n)	КД(0,05,n)	КД(0,025,n)	КД(0,01,n)
4,00	0,68	0,76	0,85	0,89
5,00	0,56	0,64	0,73	0,78
6,00	0,48	0,56	0,64	0,70
7,00	0,43	0,51	0,60	0,64
9,00	0,37	0,44	0,51	0,56
10,0	0,35	0,41	0,48	0,53
12,0	0,32	0,38	0,44	0,48
14,0	0,29	0,35	0,41	0,45
16,0	0,28	0,33	0,49	0,43
18,0	0,26	0,31	0,37	0,41
25,0	0,23	0,28	0,44	0,36
30,0	0,22	0,26	0,31	0,34

Можно вычислить по формулам

К_Д(0,1,n) (4.110)

К_Д(0,05,n) (4.111)

К_Д(0,025,n) (4.112)

К_Д(0,01,n) (4.113)

Формулы (4.110)—(4.113) справедливы при 4 ≤ n ≤ 30.

Порядок обнаружения и исключения грубых погрешно­стей и промахов с использованием критерия Диксона сводит­ся к следующему:

· значения результатов измерений сортируются в по­рядке возрастания;

· определяется расчетное (критическое) значение кри­терия Диксона по формулам (4.110)—(4.113) для принятого уровня значимости q- Кд (q,n);

· определяется значение критерия Диксона Кд по фор­муле (4.108);

· сравниваются значения Кд и Кд (q,n):

если Кд > Кд (q,n), то результат отбрасывают как содер­жащий грубую ошибку;

если Кд < Кд (q,n), то результат не содержит грубой по­грешности (промаха) с вероятностью Р = 1 - q.

Критерий β_max для исключения грубых погрешностей и промахов

При использовании этого критерия вычисляют коэффи­циенты β₁ и β₂ по формулам

(4.114)

(4.115)

Определяют β_max по таблице в зависимости от принятой вероятности Р и числа измерений п (табл. 4.8).

Таблица 4.8

Критические значения критерия β_max

n	βmax(P=0,9, n)	βmax(P=0,95, n)	βmax(P=0,99, n)
3,00	1,41	1,41	1,41
4,00	1,64	1,69	1,72
5,00	1,79	1,87	1,96
6,00	1,89	2,00	2,13
7,00	1,97	2,09	2,26
8,00	2,04	2,17	2,37
9,00	2,10	2,24	2,46
10,0	2,15	2,29	2,54
11,0	2,19	2,24	2,61
12,0	2,23	2,39	2,66
13,0	2,26	2,43	2,71
14,0	2,30	2,46	2,76
15,0	2,33	2,49	2,80
20,0	2,45	2,62	2,96
30,0	2,61	2,79	3,16
40,0	2,72	2,90	3,28
50,0	2,80	2,99	3,37

Или определяют по формулам (4.116)—(4.118), в зависи­мости от количества измерений и принятого уровня значи­мости q = 0,1; 0,05; 0,01.

Р = 1 – q(β_{max p,n}).

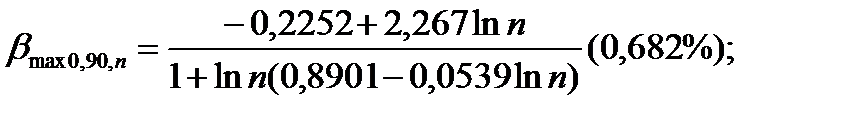(4.116)

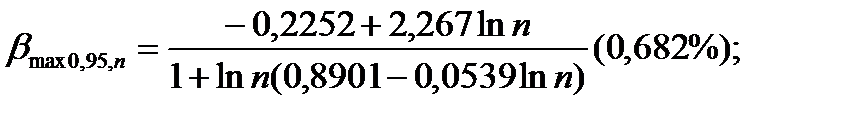(4.117) (4.118)

Формулы (4.116)—(4.118) справедливы при 3 < п < 50.

Если β₁ > β_max, то значение x _mах следует исключить из ря­да измерений как грубую погрешность.

Если β₂ < β_max, то исключают значение x _min как грубую погрешность.

Критерий Романовского для исключения грубых погрешностей и промахов

Критерий Романовского применяется, если число изме­рений п < 20. Для этого вычисляется расчетное значение критерия R _расч по формуле

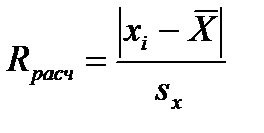(4.119)

где x_i — сомнительный результат измерения; — среднее значение результатов измерения (); — среднее квадратичное отклонение (); п – 1 – число измерений без сомнительного результата.

Расчетное значение критерия R _расч сравнивается с его критическим значением R _кр(α,n), где α — принятый уровень доверительной вероятности.

Если R _расч > R _кр(α,n), то результат х_i считается промахом и отбрасывается.

Критические значения критерия Романовского опреде­ляют по табл. 4.9.

Таблица 4.9

Значения критерия Романовского

n	q =0,01	q =0,02	q =0,05	q =0,1
	1,73	1,72	1,71	1,69
	2,16	2,13	2,10	2,00
	2,43	2,37	2,27	2,17
	2,62	2,54	2,41	2,29
	2,75	2,66	2,52	2,39
	2,90	2,80	2,64	2,49
	3,08	2,96	2,78	2,62

Или рассчитывают по формулам

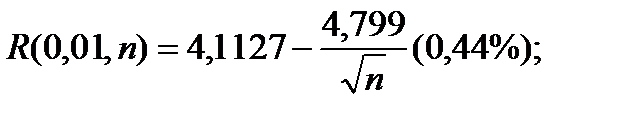(4.120)

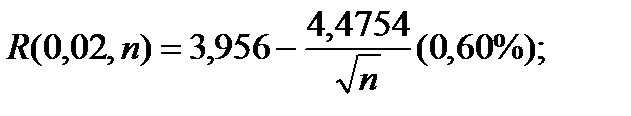(4.121)

(4.122)

(4.123)

[1] За сомнительный результат измерения принимается минимальное и максимальное значения в ряду измерений.

Дата добавления: 2015-08-31