Проецирование точки на 3 плоскости проекций

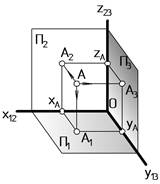
В некоторых случаях для полной характеристики формы объекта двух его проекций недостаточно. Поэтому иногда проецирование ведется на три взаимно-перпендикулярные плоскости П₁, П₂ и П₃. Эти плоскости образуют в пространстве прямоугольный трехгранник с ребрами х₁₂, y₁₃, z₂₃ (Рис. 7).

Плоскость П₃ называется профильной плоскостью проекций.

Рисунок 7

А₁ – горизонтальная проекция точки A: А₁ = АА₁ Ç П₁. Горизонтально-проецирующая прямая АА₁ перпендикулярна П₁. Отрезок AA₁ определяет координату z точки А, т.е. ее высоту.

А₂ – фронтальная проекция точки A: А₂ = АА₂ Ç П₂. Фронтально-проецирующаяпрямая АА₂ перпендикулярна П₂. Отрезок AA₂ определяет координату у точки А, т.е. ее глубину.

А₃ – профильная проекция точки A: А₃ = АА₃ Ç П₃. Прямая АА₃ перпендикулярна П₃, она называется профильно-проецирующей прямой. Отрезок AA₃ определяет координату х точки А, т.е. ее широту.

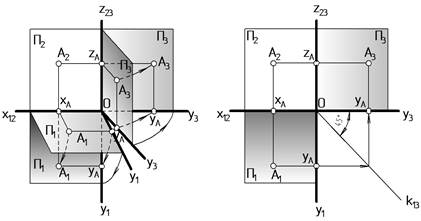
Для того, чтобы получить трехкартинный комплексный чертеж после проецирования точки одновременно осуществляют два вращения (Рис. 8 a):

· плоскость П₁ вращается вокруг оси х₁₂ по часовой стрелке на 90° до совмещения ее с плоскостью П₂, что полностью соответствует аналогичному вращению при получении двухкартинного комплексного чертежа;

· плоскость П₃ вращается вокруг оси z₂₃ против часовой стрелки на 90°, если смотреть с конца оси z₂₃, до совмещения ее с плоскостью П₂.

а б

Рисунок 8

На рис. 8 бпоказан полученный таким образом трехкартинный комплексный чертеж точки А.

Очевидно, что разворот двух плоскостей П₁ и П₃ не возможен без дублирования оси y₁₃. Одна из осей y₁ будет участвовать в повороте плоскости П₁, а вторая y₃ – П₃. Но эта условность должна обеспечивать одинаковую величину глубины точки, т.е. у₁ = у₃. Одним из графических методов, обеспечивающих эту возможность, является способ, показанный на рис. 8 б.

Под углом 45° к оси у₃ проведем прямую к₁₃, называемую постоянной прямой комплексного чертежа. Линию связи, соединяющую горизонтальную проекцию А₁ с профильной А₃, будем преломлять под прямым углом на этой прямой. Горизонтальный участок А₁y_А ^ у₁, а вертикальный А₃y_А ^ у₃.

По аналогии с двухкартинным чертежом можно доказать, что линии связи проекций точек будут перпендикулярны соответствующим осям, т.е. A₁A₂ ^ х₁₂, A₂A₃ ^ z₂₃.

На рис. 8 б: А₁А₂ ‑ вертикальная линия связи;

А₂А₃ ‑ горизонтальная линия связи;

А₁y_A и y_AА₃ ‑ ломаная линия связи;

Ox_А = y_АА₁ = z_АА₂ = х ‑ широта точки А.

Oy_А = x_АА₁ = z_АА₃ = y ‑ глубина точки А;

Oz_А = x_АА₂ = y_АА₃ = z ‑ высота точки А;

Замечание: так как плоскости не имеют границ, в совмещенном положении (на эпюре) границы их не показывают. Оси проекций фиксируют положение плоскостей проекций. Часто практически гораздо важнее установить взаимное расположение элементов оригинала (т. е. изображаемого предмета) и их форму, чем расстояния до плоскостей проекций. Поэтому, при выполнении чертежей в этих случаях оси проекций могут не изображаться или изображаться частично, подразумевая, однако, что проецирование ведется ортогональное на две или три взаимно-перпендикулярные плоскости. Линии связи при этом изображаются обязательно. Если по какой-либо причине на чертеже требуется восстановить опущенные оси проекций, то их можно провести, ориентируясь на линии связи проекций точки так, что бы х₁₂ ^ A₁A₂, z₂₃ ^. A₂A₃, а начало координат располагалось на постоянной прямой к₁₃.

Дата добавления: 2015-07-13