VI. Дискретные случайные величины. Числовые характеристики ДСВ

V. Схема Бернулли. Приближенные формулы в схеме Бернулли (формула Пуассона, формула Муавра-Лапласа). Полиномиальное распределение.

1. В среднем 20% акций на аукционе продается по первоначально заявленной стоимости. Найти вероятность того, что из 10 пакетов акций в результате торгов по первоначальной стоимости будет продано: а) ровно 5 пакетов акций; б) от 3 до 5 пакетов акций; в) более 9 пакетов акций.

2. Считая, что в среднем 15% открывающихся малых предприятий становятся банкротами в течение года, найти вероятность того, что из 5 новых малых предприятий за это время банкротами станут: а) 4 предприятия; б) не более 1 предприятия; в) хотя бы одно предприятие.

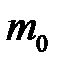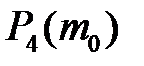3. Каждое из 4 предприятий отрасли выполняет месячный план с вероятностью 0,7. Найти вероятность того, что по истечению месяца план выполнят; а) 3 предприятия; б) менее 3 предприятий; в) найти и , где 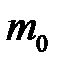- наивероятнейшее число предприятий, которые выполнили месячный план.

4. Вероятность выигрыша по билету лотереи равна 0,125. Куплено 5 билетов. Какова вероятность того, что среди них будет не менее 1 и не более 3 выигрышных билета.

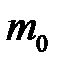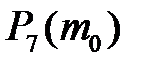5. В магазине продается 7 телевизоров марки Philips. Вероятность того, что в течение месяца будет продан один телевизор 0,8. Найти и , где 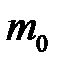- наивероятнейшее число непроданных телевизоров по истечении месяца.

6. В 5% случаев страховая компания выплачивает по договорам страховку. Найти вероятность того, что по истечению 200 договоров компания уплатит страховку: а) по 3м договорам;
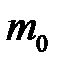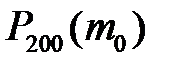б) менее чем по 2 договорам; в) хотя бы по 2м договорам; г) найти и , где 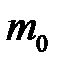- наивероятнейшее число договоров, по которым будет выплачена страховка.

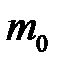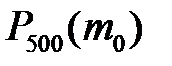7. Вероятность того, что любой из 500 пассажир опоздает к поезду, равна 0,01. Найти: а) найти и , где 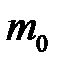- наиболее вероятное число опоздавших пассажиров; б) вероятность того, что хотя бы один пассажир опоздает к поезду.

8. Вероятность изготовления доброкачественного изделия равна 0,9. Найти вероятность того, что среди взятых наудачу 300 изделий 95% окажется доброкачественных.

9. Вероятность рождения девочки равна 0,485. Найти вероятность того, что из 600 родившихся детей: а) будет 200 мальчиков; б) девочек будет больше, чем мальчиков; в) наивероятнейшее число родившихся мальчиков.

1. Всхожесть семян некоторого растения составляет 80%. Найти вероятность того, что из 6 посеянных семян взойдут не менее трех.

11. Магазин получил 1000 бутылок шампанского. Вероятность того, что при перевозке бутылка окажется разбитой 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.

12. В электричку из 4 вагонов садятся наудачу 8 пассажиров. Какова вероятность того, что в каждый вагон вошло по 2 человека?

Ответы: I. 1. 0,3; 2. а) 3968/11781; б) 153/385; 3. 45/2431; 4. а) 1/6; б) 0,8; 5. а) 435/988; б) 244/247;
6. 913/969; 7. а) 950/2639; б) 3287/3393; 8. 13309/75670; 9. 0,72; 10. 8/253; 11. а) 0,25; б) 5/28; 12. 1/3; 13. 1/66; 14. 4200; 2/15; II. 1. 3/5; 2. (1+ln(4))/4; 3. 1/9; 4. 7/16; 5. 0,0975; III. 1. а) 132/1225; б) 946/1225; 2. 1/9; 3. а) 1/6; б) 1/30; 4. а) 0,54; б) 0,82; в) 0,18; г) 0,28; 5. а) 0,4275; б) 0,0475;
в) 0,0025; г) 0,9975; 6. а) 0,8554; б) 0,1446; в) 0,0054; 7. а) 0,48; б) 0,32; в) 0,92; 8. а) 0,08; б) 0,72;
в) 0,28; IV. 1. а) 35/300; б) 1/7; 2. а) 166/175; б) первая; 3. а) 0,815 (0,185); б) 10/163; 4. 4/7;
5. 45/101; 6. 0,3925; 7. 1273/1300; 8. третья группа; 9. 1/3; V. 1. а) 0,026; б) 0,337; в) 0,0000001;
2. а) 0,0022; б) 0,83521; в) 0,5563; 3. а) 0,4116; б) 0,1416; в) 3; 0,4116; 4. 0,4861; 5. 1; 0,367;
6. а) 0,0008; б) 0,00055; в) 0,99945; г) 10; 0,1378; 7. а) 5; 0,1745; б) 0,9933; 8. 0,001; 9. а) 0;
б) 0,2061; в) 309; 10. 0,98304; 11. 0,5767; 12. 0,038

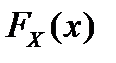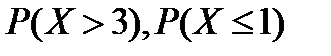1. В партии из 10 деталей содержится 2 нестандартных. Наудачу отобраны 2 детали. С.в. X – число стандартных деталей среди двух отобранных. Найти: а) ряд распределения с.в. X, функцию распределения ; б) ;в) 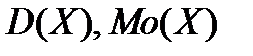; г) среднее число стандартных деталей среди двух отобранных.

2. Рабочий обслуживает два станка. Вероятность того, что за смену первый станок не сломается равна 0,9, второй – 0,8. С.в. X – число исправных станков. Найти: а) ряд распределения с.в. X, функцию распределения 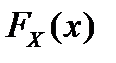; б) 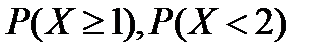; в) среднее число исправных станков;
г) .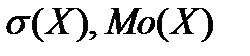

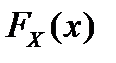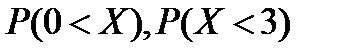3. Вероятность того, что аудитор допустит ошибку при проверке бухгалтерского баланса, равна 0,1. Аудитор проверяет 2 баланса. С.в. X – число правильных заключений на проверяемые 2 баланса. Найти: а) ряд распределения с.в. X, функцию распределения ; б) ; в) .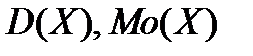

4. Стрелок делает 3 выстрела по мишени. Вероятность попадания в мишень равна 0,8. С.в. X – число попаданий по мишени при 3 выстрелах. Найти: а) ряд распределения с.в. X, функцию распределения 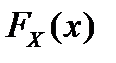; б) 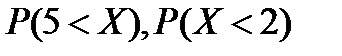; в) среднее число попаданий при трех выстрелах; г) .

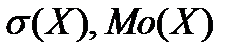5. Дискретная с.в. X задана рядом распределения:

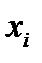
	-2	-1
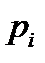
	0,2	0,2	0,1	0,3	0,2

Найти: а) 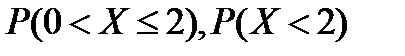; б) .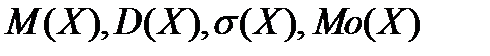

Дата добавления: 2017-01-13