ЛНДУ 2 – ого порядка

Пусть функции y1, y2,..., yn - частные решения уравнения (13). Определим число линейно независимых решений среди них..

ЛОДУ 2 – ого порядка

y’’ + p(x) y’ + q(x) y = 0 (13)

Умножим первую строчку вронскиана (12) на q(x), вторую строчку на p(x) и прибавим их к третьей строчке. В силу (13) она обратится в 0 и получаем W_n = 0. Следовательно, при частные решения линейно зависимы. Независимыми могут быть только два частных решения.

Аналогичным образом можно доказать, что ЛОДУ n – ого порядка имеет n линейно независимых решений.

Общая теорема: если у₁(х) и у₂(х) два частных линейно независимых решения однородного уравнения (13), то его общее решение имеет вид y₀ = C₁ y₁(x) + C₂ y₂(x) и содержит две произвольные константы С₁, С₂.

Условие линейной независимости частных решений можно представить в виде у₁/у₂ 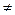const. Если y₁ = k y₂ , то в решении y₀ остается одна константа (kС₁+ C₂) и оно перестает быть общим.

y’’ + p(x) y’ + q(x) y = f(x) (14)

В правой части появляется произвольная функция f(x).

Общая теорема: пусть y*(x) - частное решение неоднородного уравнения и

y₀ - общее решение соответствующего однородного уравнения (f(x) отбрасывается). Тогда общее решение неоднородного уравнения есть сумма частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения:

y = y₀ + y* (15)

Действительно, подстановка суммы двух решений (15) в (14) приводит к двум отдельным уравнения – однородному и неоднородному.

Если известно одно частное решение однородного уравнения у₁(х), то замена

y(x) = у₁(х) z(x) dx понижает порядок ЛНДУ.

Дата добавления: 2017-01-13