Основные теоремы дифф. исчисления

Лекция № 16. 23. 12. 2016

Асимптоты.

Если при удалении точки графика в бесконечность, она сближается с некоторой прямой, то эта прямая называется асимптотой.

Так как удаление от начала координат в бесконечность может происходить как вправо/влево, так и вверх/вниз либо вообще по диагонали, то можно эту ситуацию описать одним общим условием:
Если то .

Горизонтальные асимптоты:

Если , , то асимптота горизонтальная, эта ситуация имеет место, когда .

Вертикальные асимптоты:

Если , , 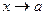то асимптота вертикальная (это соответствует разрыву 2 рода, ).

Наклонные асимптоты:

Если , , но при этом график всё же стремится к некоторой прямой, то асимптота наклонная.

Как видно, что во всех этих случаях точка неограниченно удаляется в бесконечность, но за счёт либо 1-го слагаемого, либо 2-го, либо двух сразу.

Наклонные асимптоты. Вывод формул и .

Так как точка на графике и на асимптоте сближаются то:

.

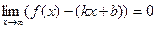Отсюда следует, что 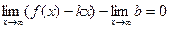, то есть

.

Рассмотрим прямую 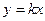, параллельную асимптоте .

Если разность ординат для точки на графике и соответствующей точки на прямой стремится к 0, то разность ординат для точки на графике и точки на прямой 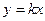стремится к . Отрезок, соответствующий этому расстоянию, отмечен красным на чертеже.

Если две величины, и , неограниченно возрастают, и при этом разность между ними не увеличивается, а стремится к константе, то их отношение стремится к 1, то есть . Но тогда .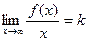

Итак, мы получили формулы для нахождения 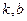. На практике сначала надо найти , а уже затем .

Пример. Найти асимптоты графика функции .

Решение. Во-первых, сразу видно точку разрыва 2-го рода 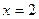. Есть вертикальная асимптота .

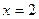Найдём наклонную асимптоту.

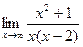(мы просто добавили лишний в знаменателе, тем самым поделили на ).

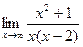= = = 1. Итак, .

Обратите внимание: здесь предел одинаково вычисляется при и при 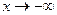, но бывают примеры, в которых по-разному, то есть на правой и левой полуплоскости могут быть разные асимптоты.

Найдём = = 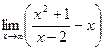= = = = 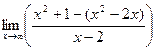2.

Ответ. Вертикальная x = 2, наклонная y = x + 2.

График выглядит так:

Замечание. При значении ситуация не однозначна: не всегда существует горизонтальная асимптота, например, для ln(x) горизонтальной асимптоты нет, несмотря на то, что 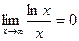. Коэффициент лишь выявляет, к чему стремится угловой коэффициент касательной. Но для ln(x) касательная стремится к горизонтальному положению, тем не менее, функция не ограничена сверху.

Замечание. Если на данной полуплоскости, правой или левой, есть наклонная асимптота, то нет горизонтальной, и наоборот, если есть горизонтальная, то нет наклонной. Действительно, ситуации (что требуется для горизонтальной асимптоты) и (при существовании наклонной, f возрастает к 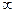) взаимоисключающие.

Замечание. Если получается , тогда нет наклонной асимтоты. Например, при 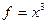, деление на ни к чему не приведёт, всё равно останется . .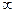

Теорема Ролля. Если функция f непрерывна и дифференцируема на [a,b], и , то существует точка , такая что .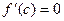

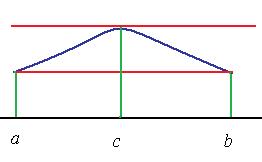
Доказательство. Если в точке такое же значение, как было в точке 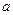, то:

1) либо функция тождественно равна константе (но тогда вообще в любой точке нулевая производная)

2) либо не константа, но тогда она должна достигать какого-то максимального отклонения от ординаты и снова возвращаться на эту же высоту, в этом случае есть точка экстремума, одна или несколько. Из теоремы Ферма об эстремуме следует, что в такой точке производная равна 0.

Теорема Лагранжа. Если функция f непрерывна и дифференцируема на [a,b], то существует точка , такая что .

Пояснение. Теорема Лагранжа фактически утверждает, что на графике есть такая точка, что касательная в ней наклонена под таким же углом, как хорда, соединяющая 2 конца графика в точках 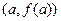и . Чертёж:

Доказательство. Рассмотрим функцию .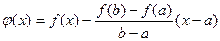

Вычислим, чему она равна в точках .

=

= = .

Итак, на концах интервала значение одно и то же. Тогда по теореме Ролля существует точка , где . Рассмотрим подробнее производную . Дробь здесь фактически просто коэффициент k, он не содержим переменную, дифференцируется только .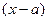

В точке с: 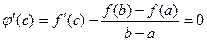, тогда .

Теорема Коши. Если функции f,g непрерывны и дифференцируемы на [a,b], то существует точка , такая что .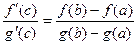

Доказательство. Рассмотрим .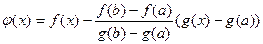

Проверим её значения на концах интервала, они одинаковы:

.

= = .

Тогда по теореме Ролля существует точка , где .

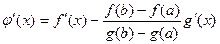, тогда ,

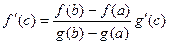, в итоге .

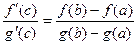Теорема Лопиталя. Функции f,g непрерывны и дифференцируемы на [a,b], и , . Тогда .

Доказательство. Если применить теорему Коши к отрезку [a,x].

В некоторой точке верно: = .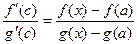

Но при 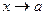, точка с, лежащая между a,x тоже стремится к а.

Тогда .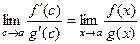

Дата добавления: 2017-01-13