Подбор параметра

Ввод и редактирование данных в режиме формы

Если таблица имеет много столбцов, которые одновременно не помещаются на экране, для ее заполнения удобно воспользоваться режимом Форма, что позволяет работать с записями в отдельном окне (в нем поочередно отображаются данные лишь одной строки).

В Excel 2007 необходимо добавить соответствующую кнопку на панель быстрого доступа: щелкнуть кнопку Настройка панели быстрого доступа (вверху слева), выбрать пункт Другие команды. Далее (вверху слева) в поле Выбрать команды выбрать Все команды, в списке ниже выбрать Форма, Добавить, ОК.

Для открытия окна формы надо щелкнуть в любую ячейку таблицы и нажать кнопку Форма на панели быстрого доступа. Переход между строками – с помощью Назад и Далее. Добавление и удаление записей – Добавить и Удалить. Поиск записей осуществляется с помощью кнопки Критерии (Ввести значение, ENTER, выход – с помощью кнопки Правка).

Скрытие (и отображение) строк /столбцов.

Выделить строки, на Главная-Ячейки нажать Формат. В списке выбрать скрыть (или отобразить), в подменю выбрать Скрыть строки.

Для возврата строк: выделить строки, прилегающие к скрытым. Далее аналогично предыдущему.

Задачу, которая может быть решена с помощью П одбора параметров можно представить следующим образом. Есть формула (или цепочка последовательно зависящих друг от друга формул), значение которой зависит от значения одного параметра х. Требуется найти значение х, которое обеспечивает заданное значение формулы.

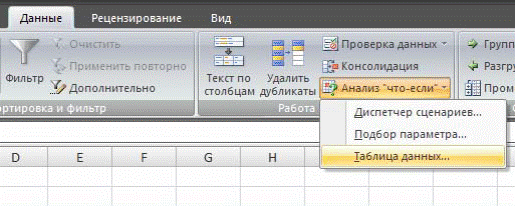
На Данные-Работа с данными щелкнуть на нижнем черном треугольнике раскрывающегося списка (Анализ «что если»), выбрать Подбор параметра, в поле Установить в ячейке ввести ссылку на ячейку, содержащую формулу, в поле Значение ввести заданное значение (которое должно быть достигнуто). В поле Изменяя значение ячейки ввести ссылку на ячейку, значение которой нужно подобрать (т.е. содержащей искомое значение параметра). Упомянутая формула должна ссылаться на эту ячейку.

Если задача имеет несколько решений (несколько значений х, обеспечивающих заданное значение формулы, то в ячейку с х следует предварительно ввести ориентировочное значение х.

Пример: решение квадратного уравнения ax²+bx+c=0.

В ячейки A2,B2,C2 вводим значения a,b,c. В ячейку D2 вводим приближенное значение х. Вводим в ячейку E2 формулу =A2*D2^2+B2*D2+C2. На Данные-Работа с данными щелкнуть треугольник внизу справа, Подбор параметров. В поле Установить в ячейке указываем E2, в поле Значение указываем 0 (число ноль), а в поле Изменяя значение указываем D2. Жмем на OK. Для примерной локализации корней предварительно можно построить график функции у = ax²+bx+c (координаты пересечения кривой с осью Х).

Инструмент Excel Поиск решения

Используется для решения ряда актуальных задач, в частности, оптимизационных задач.

Для этого в Excel применяется надстройка Поиск решения. Для ее подключения (если она не была подключена ранее) следует нажать последовательно кнопки: Office (в левом верхнем углу окна Excel), Параметры Excel, Надстройки. В соответствующем окне в поле Управление выбрать Надстройки Excel, Перейти и в поле Надстройки включить флажок Поиск решения, нажать кнопку ОК.

Использование инструмента Поиск решения для нахождения наименьшего (или наибольшего) значения функции

В выбранные ячейки (например, А1 и В1) ввести начальные приближения для аргументов функции и формулу для функции (например, «=А1^2+В1^2»). На вкладке Данные-Анализданных выбрать Поиск решения. В диалоговом окне Поиск решения в поле Установить целевую ячейку надо указать ссылку на ячейку с формулой для функции, в поле Изменяя ячейки ввести адреса ячеек со значениями аргументов. Затем отметить радио-кнопку минимальному (или максимальному) значению. Если имеются ограничения на значения переменных, (например, x > 1 и y >2), то: в окне Поиск решения нажать кнопку Добавить, в появившемся окне Добавление ограничения в поле Ссылка на ячейку вписать адрес ячейки, содержащей x, в среднее поле вписать знак >, в поле Ограничение вписать число 1, и аналогично для y. Нажать Выполнить.

Вариант более сложного ограничения (например, 2x+3y > 4) см. ниже.

Использование инструмента Поиск решения для решения задачи линейного программирования

Рассматривается линейная функция нескольких аргументов f(Х) 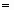с₁x₁ + с₂x₂+...+с_nx_n. Требуется найти значения переменных Х = (х₁,…, х_n), доставляющие максимальное или минимальное значение функции f(х₁,…, х_n) при наличии нескольких (m) линейных же (относительно аргументов) ограничений:

φ_i(х₁,…, х_n) {≤, =, ≥ } b_i; (i=1,…,m)

Например, найти значения х_1, х₂, доставляющие максимальное значение функции f=4х₁+2х₂ при наличии ограничения φ(х₁, х₂)=2х₁+5х₂ ≤ 4.

Как правило, налагаются также условия неотрицательности:

х_j ≥ 0 (j=1,…s, s ≤ n).

Следует отметить, что в общем случае в Excel для решения задачи линейного программирования используется симплекс-метод.

Пример 1. Требуется найти значения переменных х и у, которые обеспечивают максимальное значение линейной целевой функции f(x,y)=2x+3y при наличии линейных ограничений: x+2y <= 4, 2x+y <= 3 а также x >= 0, y >= 0.

Решение. Ячейки А1 и В1 отводим под значения х и у. В ячейку А2 вводим формулу «= 2*А1+3*В1», в А3 вводим «=А1+2*В1», в ячейку А4 вводим «= 2*А1+В1». На вкладке Данные-Анализ выбираем Поиск решения. В диалоговом окне Поиск решения в поле Установить целевую ячейку вводим ссылку «А2», в поле Изменяя ячейки вводим «A1:B1». Далее нажимаем Добавить в списке Ограничения. Появится диалоговое окно Добавление ограничения. В его поле Ссылка на ячейку (для ограничения x+2y <=4) вводим адрес «А3», затем (правее) выбираем операцию сравнения <=, затем в поле Ограничение задаем константу 0 (или, в общем случае, ссылку на ячейку со значением или формулой). Кнопка ОК добавляет ограничение и закрывает окно. Для ограничения 2x+y <= 3: Добавить, в поле Ссылка на ячейку вводим «А4», затем выбираем операцию сравнения <=, затем в поле Ограничение задаем константу 3.

Примечание: приведенные ниже иллюстрации содержат данные другой задачи.

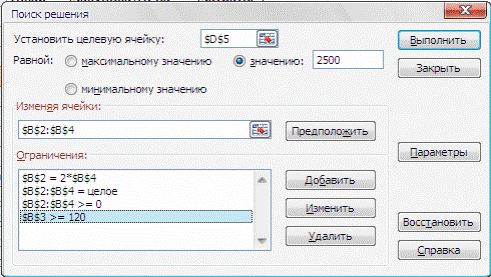
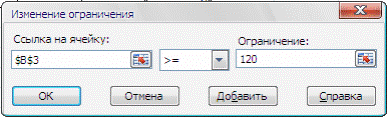
Щелкаем Параметры. В окне Параметры поиска решения ставим флажок Неотрицательные значения для переменных x и y. Флажок Линейная модель следует устанавливать для решения задач, в которых отсутствуют нелинейные зависимости (и в целевой функции и в ограничениях), что облегчает решение линейной задачи. (Можно задать также максимальное время на решение, предельное число итераций, относительную погрешность.) После того, как все данные для инструмента Поиск решения будут заданы, следует нажать кнопку Выполнить.

Внимание!: В окне Добавление ограничения, помимо операций <= и >=, доступны условия: целочисленности (“цел”) и двоичности (“двоич”). При выборе “цел” переменные могут принимать только целые значения (например, число станков), При выборе “ двоич” – значения 0 или 1 (Например, при выборе из пяти станков два мы вводим пять соответствующих двоичных переменных. При этом, например, значение “1” для 2-й переменной будет означать использование 2-го станка, “0” - неиспользование).

Дата добавления: 2017-01-13