
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычислить определитель 2 страница
|
|
|
|
 .
.
В нашем случае для точки 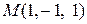 и вектора
и вектора 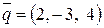 получаем:
получаем:
 ,
,
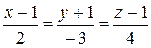 .
.
Найдем точку пересечения прямой и плоскости. Для этого запишем уравнение прямой в параметрическом виде:



Подставим полученные выражения для x, y, z в уравнение плоскости:
 ,
,
 ,
,
 ,
,
 .
.
Подставим полученное значение t в параметрическое уравнение прямой, и, тем самым, найдем координаты точки М 1 пересечения прямой L и плоскости p, т.е. координаты проекции точки М на плоскость p:
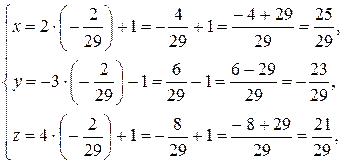
 .
.
Ответ:  .
.
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
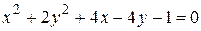 .
.
Решение:
Выделим в правой части уравнения полные квадраты относительно х и у:
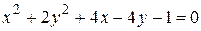 ,
,
 ,
,
 ,
,
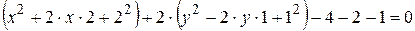 ,
,
 ,
,
 .
.
Получили каноническое уравнение эллипса с центром в точке Q 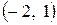 и полуосями
и полуосями  и
и  .
.
Построим эллипс с данными параметрами.

| Вариант 1 | |
1. Вычислить произведение матриц
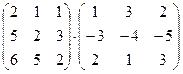 .
2. Вычислить определитель .
2. Вычислить определитель
 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
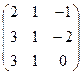 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
 б) Методом Крамера.
б) Методом Крамера.
 в) Методом Гаусса.
в) Методом Гаусса.
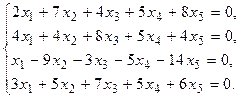 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 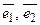 : :

| 6. Установить, являются ли векторы 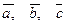 линейно-зависимыми: линейно-зависимыми:
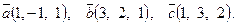 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(2,-3), М2(3, 4) и найти расстояние от точки P(0, 2) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2,-3), М2(3, 4) и найти расстояние от точки P(0, 2) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически

|
| Вариант 2 | |
1. Вычислить произведение матриц
 .
2. Вычислить определитель .
2. Вычислить определитель
 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
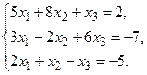 б) Методом Крамера.
б) Методом Крамера.
 в) Методом Гаусса.
в) Методом Гаусса.
 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 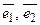 : :

| 6. Установить, являются ли векторы 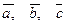 линейно-зависимыми: линейно-зависимыми:
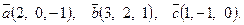 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(1,-2), М2(-2, 2) и найти расстояние от точки Р(3, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(1,-2), М2(-2, 2) и найти расстояние от точки Р(3, 1) до полученной прямой.
9. Найти угол между прямыми
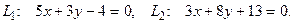 10. От общего уравнения прямой
10. От общего уравнения прямой
 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
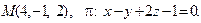 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически

|
| Вариант 3 | |
1. Вычислить произведение матриц
 .
2. Вычислить определитель .
2. Вычислить определитель
 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
 б) Методом Крамера.
б) Методом Крамера.
 в) Методом Гаусса.
в) Методом Гаусса.
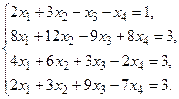 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 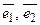 : :

| 6. Установить, являются ли векторы 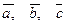 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
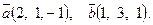 8. Составить уравнение прямой, проходящей через две точки М1(-2,-2), М2(0, 4) и найти расстояние от точки Р(-2, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(-2,-2), М2(0, 4) и найти расстояние от точки Р(-2, 1) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
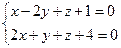 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
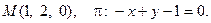 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
| Вариант 4 | |
1. Вычислить произведение матриц
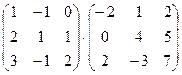 .
2. Вычислить определитель .
2. Вычислить определитель
 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
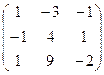 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
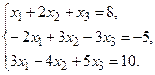 б) Методом Крамера.
б) Методом Крамера.
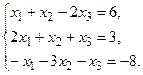 в) Методом Гаусса.
в) Методом Гаусса.
 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 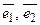 : :

| 6. Установить, являются ли векторы 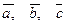 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(5, 4) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(5, 4) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
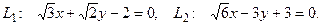 10. От общего уравнения прямой 10. От общего уравнения прямой 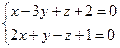 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
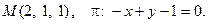 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
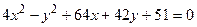 . .
|
| Вариант 5 | |
1. Вычислить произведение матриц
 .
2. Вычислить определитель .
2. Вычислить определитель
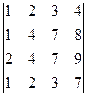 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
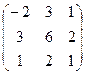 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
 б) Методом Крамера.
б) Методом Крамера.
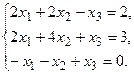 в) Методом Гаусса.
в) Методом Гаусса.
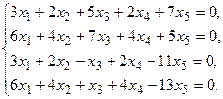 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 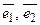 : :
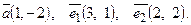
| 6. Установить, являются ли векторы 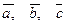 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(2,-2), М2(0, 3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2,-2), М2(0, 3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
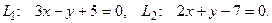 10. От общего уравнения прямой
10. От общего уравнения прямой
 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
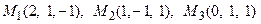 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
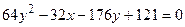 . .
|
| Вариант 6 | |
1. Вычислить произведение матриц
 .
2. Вычислить определитель .
2. Вычислить определитель
 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
 б) Методом Крамера.
б) Методом Крамера.
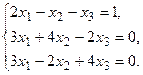 в) Методом Гаусса.
в) Методом Гаусса.
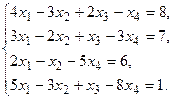 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 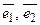 : :
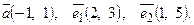
| 6. Установить, являются ли векторы 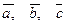 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(1,-3) и найти расстояние от точки Р(-1, 0) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(3,-2), М2(1,-3) и найти расстояние от точки Р(-1, 0) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
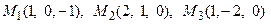 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
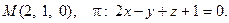 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
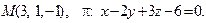 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
| Вариант 7 | |
1. Вычислить произведение матриц
 .
2. Вычислить определитель .
2. Вычислить определитель
 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
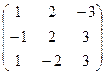 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
 б) Методом Крамера.
б) Методом Крамера.
 в) Методом Гаусса.
в) Методом Гаусса.
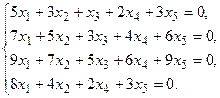 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 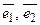 : :

| 6. Установить, являются ли векторы 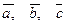 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
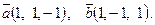 8. Составить уравнение прямой, проходящей через две точки М1(4,-2), М2(2,-3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(4,-2), М2(2,-3) и найти расстояние от точки Р(-1, 1) до полученной прямой.
9. Найти угол между прямыми
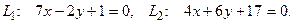 10. От общего уравнения прямой
10. От общего уравнения прямой
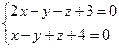 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
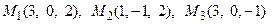 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
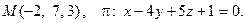 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
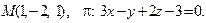 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
| Вариант 8 | |
1. Вычислить произведение матриц
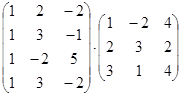 .
2. Вычислить определитель .
2. Вычислить определитель
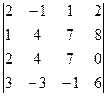 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
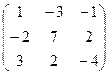 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
 б) Методом Крамера.
б) Методом Крамера.
 в) Методом Гаусса.
в) Методом Гаусса.
 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 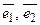 : :
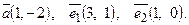
| 6. Установить, являются ли векторы 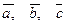 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
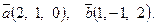 8. Составить уравнение прямой, проходящей через две точки М1(1, 5), М2(2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(1, 5), М2(2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
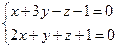 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
| Вариант 9 | |
1. Вычислить произведение матриц
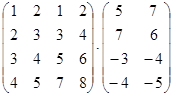 .
2. Вычислить определитель .
2. Вычислить определитель
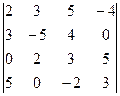 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
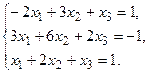 б) Методом Крамера.
б) Методом Крамера.
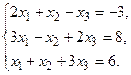 в) Методом Гаусса.
в) Методом Гаусса.
 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 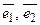 : :

| 6. Установить, являются ли векторы 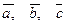 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
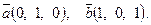 8. Составить уравнение прямой, проходящей через две точки М1(2, 5), М2(-2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(2, 5), М2(-2, 2) и найти расстояние от точки Р(1, 1) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
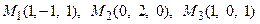 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
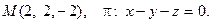 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
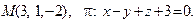 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
| Вариант 10 | |
1. Вычислить произведение матриц
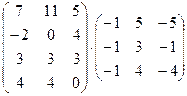 .
2. Вычислить определитель .
2. Вычислить определитель
 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
 б) Методом Крамера.
б) Методом Крамера.
 в) Методом Гаусса.
в) Методом Гаусса.
 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 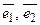 : :

| 6. Установить, являются ли векторы 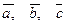 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(0, 5), М2(-2, 2) и найти расстояние от точки Р(2, 0) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(0, 5), М2(-2, 2) и найти расстояние от точки Р(2, 0) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
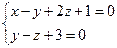 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
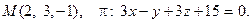 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
 . .
|
| Вариант 11 | |
1. Вычислить произведение матриц
 .
2. Вычислить определитель .
2. Вычислить определитель
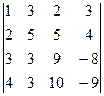 .
3. Найти обратную матрицу .
3. Найти обратную матрицу
 .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы. .
4. Решить системы линейных уравнений.
а) Методом обратной матрицы.
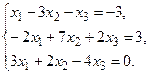 б) Методом Крамера.
б) Методом Крамера.
 в) Методом Гаусса.
в) Методом Гаусса.
 5. Написать разложение вектора
5. Написать разложение вектора  по базису по базису 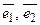 : :

| 6. Установить, являются ли векторы 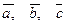 линейно-зависимыми: линейно-зависимыми:
 7. Найти площадь параллелограмма, построенного на векторах
7. Найти площадь параллелограмма, построенного на векторах  и и  : :
 8. Составить уравнение прямой, проходящей через две точки М1(1, 0), М2(2, -3) и найти расстояние от точки Р(2, 3) до полученной прямой.
9. Найти угол между прямыми
8. Составить уравнение прямой, проходящей через две точки М1(1, 0), М2(2, -3) и найти расстояние от точки Р(2, 3) до полученной прямой.
9. Найти угол между прямыми
 10. От общего уравнения прямой
10. От общего уравнения прямой
 перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
перейти к каноническому уравнению.
11. Написать уравнение плоскости, проходящей через три заданные точки
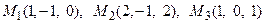 .
12. Найти расстояние от точки М до плоскости p: .
12. Найти расстояние от точки М до плоскости p:
 13. Найти проекцию точки М на плоскость p:
13. Найти проекцию точки М на плоскость p:
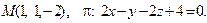 14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
14. Привести уравнение кривой второго порядка к каноническому виду и изобразить графически
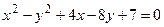 . .
|
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 256; Нарушение авторских прав?; Мы поможем в написании вашей работы!