
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методические указания 1 страница
|
|
|
|
Решение
Введение
Брянск 2012
Методические указания предназначены
Примеры выполнения.
Линейное программирование
Брянск 2012
Методические указания предназначены
Пример выполнения.
Линейное программирование
Буров П.А, Муравьев А.Н.
Аналитическая геометрия
Линейная алгебра.
Шерягин Иван Васильевич
Савченко Евгения Викторовна
Лобанова Ирина Станиславовна
Учебное пособие
Компьютерный набор и верстка авторов
Подготовка к печати Н.Н. Завернина
Сдано в производство 08.06.05 г. Подписано в печать 15.06.2005 г.
Уч.-изд. л. 1,77. Формат 84х1081/16. Усл.-печ. л. 5,5.
Изд. №785. Заказ №762.
Редакционно-издательский отдел Севмашвтуза
164500, г. Северодвинск, ул. Воронина, 6.
Сведения из теории,
методические указания к выполнению РГР,
для студентов экономического факультета.

Министерство высшего образования РФ
Брянская государственная инженерно-технологическая академия
Кафедра математики
Утверждены научно- методическим советом БГИТА
Протокол N__ от ________
Сведения из теории,
методические указания к выполнению РГР,
для студентов экономического факультета
Авторы: Буров Петр Алексеевич,
Муравьев Анатолий Николаевич
Рецензент: к.т.н., доцент БГИТА Миленин Н.К.
Рекомендованы: учебно-методической комиссией
механического факультета
Протокол № ___ от ___ 2012г.
Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и методов их решения. В общем случае постановка задачи математического программирования состоит в нахождении наибольшего или наименьшего (экстремального) значения функции  , при условиях
, при условиях 
 , где
, где  и
и  заданные функции, а
заданные функции, а  - заданные действительные числа. Функция
- заданные действительные числа. Функция  называется целевой функцией, а система неравенств
называется целевой функцией, а система неравенств 
 называется системой ограничений.
называется системой ограничений.
Если  и
и  линейные функции, то соответствующая задача математического программирования называется задачей линейного программирования (ЗЛП).
линейные функции, то соответствующая задача математического программирования называется задачей линейного программирования (ЗЛП).
Основная задача линейного программирования и ее свойства
Основной (канонической) задачей линейного программирования называется задача состоящая в нахождении неотрицательного решения системы  уравнений с
уравнений с  неизвестными (система ограничений)
неизвестными (система ограничений)
 (1)
(1)
при котором целевая функция 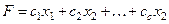 (2) принимает максимальное
(2) принимает максимальное
значение. Из алгебры известно, что система линейных уравнений имеет решение, если ранг матрицы системы равен рангу ее расширенной матрицы, т.е.  .
.
Если к тому же  , то система имеет единственное решение, и, если это решение является допустимым, то оно и является оптимальным. Если
, то система имеет единственное решение, и, если это решение является допустимым, то оно и является оптимальным. Если  , то система имеет бесчисленное множество решений. В этом случае
, то система имеет бесчисленное множество решений. В этом случае  неизвестных объявляются свободными (им придают произвольные значения), а остальные
неизвестных объявляются свободными (им придают произвольные значения), а остальные 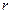 неизвестных выражаются через свободные.
неизвестных выражаются через свободные.
Любое неотрицательное решение системы ограничений называется допустимым решением или допустимым планом. План 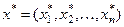 при котором целевая функция
при котором целевая функция  принимает максимальное значение называется оптимальным планом.
принимает максимальное значение называется оптимальным планом.
Переменные входящие только в одно уравнение системы с коэффициентом +1 называется базисным.
Допустимое решение  при котором свободные переменные равны нулю, а базисные переменные неотрицательны, называется опорным базисным решением.
при котором свободные переменные равны нулю, а базисные переменные неотрицательны, называется опорным базисным решением.
Множество решений задачи линейного программирования, если оно не пусто, является выпуклым множеством, то есть образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный план.
Графический метод решения ЗЛП
Если целевая функция и система ограничений являются функциями только двух переменных, то ЗЛП можно решить графическим или геометрическим методом. При этом методе поступают следующим образом:
1. Строят область допустимых решений (О.Д.Р.), т. е. область решений системы ограничений.
2. Строят линии уровня целевой функции  .
.
3. Строят вектор градиента целевой функции  , т.е.
, т.е.  , указывающий направление наискорейшего возрастания целевой функции.
, указывающий направление наискорейшего возрастания целевой функции.
4. Передвигают линии уровня в направлении вектора  , находят точки области допустимых решений через которые проходят линии наивысшего и наинизшего уровней.
, находят точки области допустимых решений через которые проходят линии наивысшего и наинизшего уровней.
5. Вычисляя значения функции  в этих точках, находят
в этих точках, находят  и
и 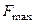 .
.
Рассмотрим пример. Среди всех неотрицательных решений системы неравенств
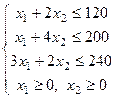
найти такое, при котором целевая функция  принимает максимальное значение.
принимает максимальное значение.
1. Так как все неравенства в системе ограничений и целевая функция являются линейными, то данная задача является задачей линейного программирования. Решим ее графическим методом. Построим область допустимых решений. Для этого построим область решения каждого из неравенств. Заменяя знаки неравенств на знаки точных равенств, строим соответствующие прямые. Каждая прямая разбивает плоскость на две полуплоскости. Для одной из них выполняется знак  , для другой
, для другой  . Чтобы определить знак неравенства для полуплоскости, из нее берется какая-то точка (контрольная) и ее координаты подставляем в соответствующее неравенство:
. Чтобы определить знак неравенства для полуплоскости, из нее берется какая-то точка (контрольная) и ее координаты подставляем в соответствующее неравенство:  ;
; 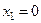 ,
, 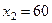 ;
; 
 ,
, 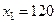 . Возьмем контрольную точку О(0; 0) и подставим ее в неравенство
. Возьмем контрольную точку О(0; 0) и подставим ее в неравенство  . Получим
. Получим  , неравенство справедливо и, следовательно, полуплоскость определяемая этим неравенством содержит точку О(0;0). Отметим эту полуплоскость. Аналогично находим области решения второго и третьего неравенств.
, неравенство справедливо и, следовательно, полуплоскость определяемая этим неравенством содержит точку О(0;0). Отметим эту полуплоскость. Аналогично находим области решения второго и третьего неравенств.  ,
, 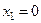 ,
,  ;
;  ,
,  .
. 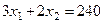 ,
, 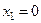 ,
,  ;
;  ,
, 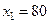 . Объединяя области решений этих трех неравенств, видим, что областью допустимых решений является многоугольник OABCD.
. Объединяя области решений этих трех неравенств, видим, что областью допустимых решений является многоугольник OABCD.

2. Построим линии уровня целевой функции  . Положим
. Положим  . Соответствующая линия уровня будет:
. Соответствующая линия уровня будет: 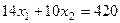 . Пусть
. Пусть  ,
,  и
и 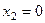 ,
,
 .
.
3. Из начала координат построим вектор  , указывающий направление наискорейшего возрастания функции
, указывающий направление наискорейшего возрастания функции  .
.
4. Передвигая линии уровня целевой функции в направлении вектора  , видим, что максимальное значение функция
, видим, что максимальное значение функция  принимает в точке
принимает в точке  . Найдем координаты этой точки из решения системы уравнений:
. Найдем координаты этой точки из решения системы уравнений:  ,
,  ;
;  ,
,  ,
,  .
.
5. Подставим координаты точки  в целевую функцию:
в целевую функцию: 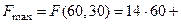
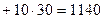
Развернутый симплексный метод
Суть этого метода состоит в переходе от одного опорного решения к другому при условии, что значение целевой функции при этом будет увеличиваться. Идею этого метода рассмотрим на примере решения предыдущей задачи:
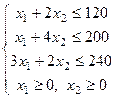

Решение. Перейдем к основной задаче линейного программирования путем введения дополнительных неотрицательных переменных  , то есть от системы ограничений вида неравенств перейдем к системе ограничений вида равенств.
, то есть от системы ограничений вида неравенств перейдем к системе ограничений вида равенств.

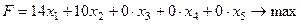
Ранг матрицы системы уравнений равен рангу ее расширенной матрицы и равен 3, следовательно, система имеет множество решений. Число свободных переменных равно  . Пусть это будут
. Пусть это будут  и
и  . Переменные
. Переменные  - базисные. Выразим базисные переменные через свободные:
- базисные. Выразим базисные переменные через свободные:  . Придавая свободным переменным нулевые значения, получим первое опорное решение:
. Придавая свободным переменным нулевые значения, получим первое опорное решение:  ,
,  . Так как коэффициенты при неизвестных
. Так как коэффициенты при неизвестных  и
и  в целевой функции положительны, то значения ее можно увеличить за счет увеличения значений переменных
в целевой функции положительны, то значения ее можно увеличить за счет увеличения значений переменных  и
и  . Так как коэффициент при
. Так как коэффициент при  больше, то будем увеличивать значение
больше, то будем увеличивать значение  за счет увеличения
за счет увеличения  . Сделаем переменную
. Сделаем переменную  базисной переменной. Из выражения для
базисной переменной. Из выражения для  видим, что
видим, что  можно увеличивать до 120; из выражения для
можно увеличивать до 120; из выражения для 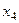 видим, что
видим, что  можно увеличивать до 200; из выражения для
можно увеличивать до 200; из выражения для  видим, что
видим, что  можно увеличивать до
можно увеличивать до  . Сравнивая эти значения, выбираем наименьшее из них:
. Сравнивая эти значения, выбираем наименьшее из них:  , иначе переменные
, иначе переменные  ,
, 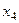 могут стать отрицательными. Это значение соответствует базисной переменной
могут стать отрицательными. Это значение соответствует базисной переменной  и ее определим свободной.
и ее определим свободной.  ,
, 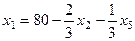 . Подставляя это значение в выражения для
. Подставляя это значение в выражения для  ,
, 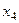 и
и  , получим:
, получим: 
 ,
,  .
.
Придавая свободным переменным  и
и  нулевые значения, получим опорное решение
нулевые значения, получим опорное решение  .
.
Так как коэффициент при  в целевой функции
в целевой функции  положителен, то ее значение можно увеличивать за счет увеличения переменной
положителен, то ее значение можно увеличивать за счет увеличения переменной  и ее определим базисной. Для определения свободной переменной найдем
и ее определим базисной. Для определения свободной переменной найдем  =30.
=30.
Оно соответствует базисной переменной  и ее определим свободной.
и ее определим свободной.  ;
;  . Подставим это в выражения для
. Подставим это в выражения для  ,
, 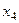 и
и  .
. 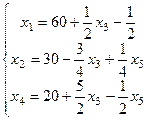
 .
.
Придавая свободным переменным  и
и  нулевые значения, получим опорное решение:
нулевые значения, получим опорное решение:  ,
,  .
.
Так как коэффициенты при неизвестных в целевой функции  отрицательны, то дальнейшее увеличение целевой функции невозможно. Итак,
отрицательны, то дальнейшее увеличение целевой функции невозможно. Итак,  ,
,  .
.
Симплексный метод
Симплексный метод решения ЗЛП состоит в переходе от одного опорного решения к другому, при котором значение целевой функции возрастает при условии, что данная задача имеет оптимальный план. Этот переход возможен, если известен какой-то исходный опорный план. Пусть требуется найти максимум функции  при условиях
при условиях


Здесь  - заданные числа, причем
- заданные числа, причем 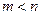 и
и 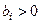 .
.
Запишем эту задачу в векторной форме. Найти  при условиях
при условиях  , где
, где  ,
, 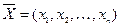 ,
, 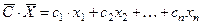 - скалярное произведение,
- скалярное произведение,  и
и  -
-  - мерные векторы-столбцы, составленные из коэффициентов при неизвестных и свободных членов.
- мерные векторы-столбцы, составленные из коэффициентов при неизвестных и свободных членов.
 ;
;  ; …..
; …..  ;
;  ; …..;
; …..;  ;
;  .
.
Данная задача имеет невырожденный опорный план  . Система векторов
. Система векторов  имеет ровно
имеет ровно  единичных векторов
единичных векторов  , которые образуют базис. Любой вектор
, которые образуют базис. Любой вектор  может быть единственным образом представлен в виде линейной комбинации базисных векторов. Сформулируем признак оптимальности опорного плана. Положим
может быть единственным образом представлен в виде линейной комбинации базисных векторов. Сформулируем признак оптимальности опорного плана. Положим  ,
, 
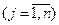 .
.
Теорема 1. Опорный план  является оптимальным планом ЗЛП, если
является оптимальным планом ЗЛП, если  .
.
Теорема 2. Если существует 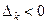 для некоторого
для некоторого  , но среди чисел
, но среди чисел  нет положительных, то целевая функция не ограничена на множестве ее планов.
нет положительных, то целевая функция не ограничена на множестве ее планов.
Теорема 3. Если опорный план  не вырожден и существует
не вырожден и существует 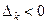 , но среди чисел
, но среди чисел 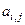 есть положительные, то существует опорный план
есть положительные, то существует опорный план  такой, что
такой, что 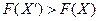 .
.
Эти теоремы позволяют проверять опорный план на оптимальность. Симплексный метод дает алгоритм перехода от одного опорного плана к другому. Рассмотрим алгоритм табличного симплекс-метода. Пусть среди  есть отрицательные. Выбираем из них наименьшее. Пусть это будет
есть отрицательные. Выбираем из них наименьшее. Пусть это будет 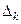 . Тогда вектор
. Тогда вектор  будем вводить в базис. Столбец соответствующий этому вектору называется направляющим. Для выбора вектора выводимого из базиса находим
будем вводить в базис. Столбец соответствующий этому вектору называется направляющим. Для выбора вектора выводимого из базиса находим  для
для  . Пусть это
. Пусть это  соответствует
соответствует  , следовательно, вектор
, следовательно, вектор  будем выводить из базиса. Строка соответствующая вектору
будем выводить из базиса. Строка соответствующая вектору  называется направляющей, а элемент
называется направляющей, а элемент  стоящий на пересечении направляющего столбца и направляющей строки называется разрешающим. Заполнение следующей таблицы начинаем с заполнения направляющей строки путем деления всех ее элементов на разрешающий. Остальные элементы таблицы рассчитываются по формулам Жордана-Гаусса:
стоящий на пересечении направляющего столбца и направляющей строки называется разрешающим. Заполнение следующей таблицы начинаем с заполнения направляющей строки путем деления всех ее элементов на разрешающий. Остальные элементы таблицы рассчитываются по формулам Жордана-Гаусса:
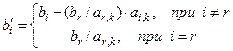 ,
,  ,
,
 ;
;  .
.
Этот процесс продолжается до тех пор, пока среди  не останется отрицательных. Рассмотрим алгоритм табличного симплекс-метода на примере решения предыдущей задачи.
не останется отрицательных. Рассмотрим алгоритм табличного симплекс-метода на примере решения предыдущей задачи.
Пусть требуется найти максимум функции 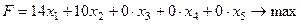 при ограничениях:
при ограничениях:  . Запишем систему ограничений в векторной форме:
. Запишем систему ограничений в векторной форме:  , где
, где
векторы:  ;
;  ;
; 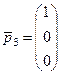 ;
;  ;
;  ;
;  .
.
Среди системы векторов  есть ровно три единичных вектора
есть ровно три единичных вектора  , которые образуют базис. Задача имеет невырожденный опорный план
, которые образуют базис. Задача имеет невырожденный опорный план  и ее можно решить табличным симплекс-методом. Составим симплекс-таблицы:
и ее можно решить табличным симплекс-методом. Составим симплекс-таблицы:
| № табл. | i | базис | 
| 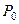
| 
| |||||

| 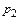
| 
| 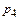
| 
| ||||||
| I | P3 P4 P5 |  200/1=200
240/3=80
200/1=200
240/3=80
| ||||||||
| m+1 | 
| -14 | -10 | |||||||
| II | P3 P4 P1 | 4/3 10/3 2/3 | -1/3 -1/3 1/3 | |||||||
| m+1 | 
| -2/3 | 14/3 | |||||||
| III | P2 P4 P1 | 3/4 -5/2 -1/2 | -1/4 1/2 1/2 | |||||||
| m+1 | 
| 1/2 | 9/2 |
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 250; Нарушение авторских прав?; Мы поможем в написании вашей работы!