Правила решения уравнений и систем уравнений с одним неизвестным в алгебре множеств

Операции над множествами

В этом разделе приведены основные соотношения алгебры множеств, используемые для решения задач теории множеств.

1a) AUB = BUA 1b) A*B = B*A

2a) AU(BUC) = (AUB)UC 2b) A*(B*C) = (A*B)*C

3a) AUB*C = (AUB)*(AUC) 3b) A*(BUC) = ABUAC

4a) AUФ = A 4b) A*E = A

5a) 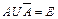5b)

6a) AUE = E 6b) A*Ф = Ф

7a) 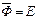7b)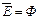

8a) AUA = A 8b) A*A = A

9a) AUAB = A 9b) A*(AUB) = A

10a) 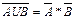10b)

11)Если AUB = E и AB = Ф, то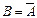

12)

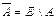
13)

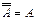
14)

15)

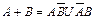
16) A+B = B+A

17) (A+B)+C = A+(B+C)

18) A+Ф = Ф +A = A

19)

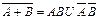
20) AB+AC = A(B+C)

21) A Ì B, если только AB=A, либо AUB=A, либо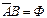

22) A=B, если и только если A+B = Ф

23)

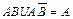
24)

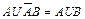
25)

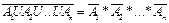
26)

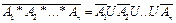
Приведенные тождества отражают определенные свойства операций над множествами, причем, они справедливы независимо от конкретного содержания входящих в них множеств, являющихся подмножествами универсума E.

Тождества (1а)-(3а) выражают коммутативный, ассоциативный и дистрибутивный законы для объединения, а (1b)-(3b) – те же законы для пересечения. Соотношения (4а)-(7а) определяют свойства пустого множества Ф и универсума Е относительно объединения, а (4b)-(7b) – относительно пересечения.

Выражения (8а) и (8b), называемые законами идемпотентности, позволяют записывать формулы с множествами без коэффициентов и показателей степени.

Формулы (9а) и (9b) и (24) – это законы поглощения, (10а) и (10b) – законы де Моргана, а (23) – закон склеивания.

Соотношения (11)-(22) отражают свойства дополнения, разности, дизъюнктивной суммы, включения и равенства.

1) Всоответствии с соотношением (22), исходноеуравнениеприводится к виду, содержащему пустое множество в правой части.

2) Полученное уравнение преобразуется к виду 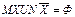, где M и N – некоторые множества или выражения в алгебре множеств, не содержащие Х. Несложно показать, что уравнение с пустой правой частью приводится к указанному виду.

3) На основании полученного уравнения и соотношения (21) записывается решение в виде: N Ì X Ì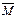

Пример 1 Решить уравнение XUC = D, C Í D.

Используя (22), получаем (XUC)+D = Ф. Используя (15), убираем в полученном уравнении знак «+». Получим:

(XUC)+D=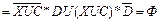

В соответствии с теоремой Де Моргана (10а) раскрываем скобки:

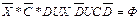
Используя условие C Í D, получаем 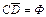. Таким образом, уравнение приводится к виду: 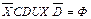, откуда решение записывается так: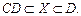

Пример 2 Решить уравнение

Далее используются (19), (13), (14) и (10b):

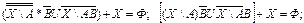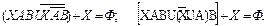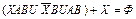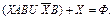Раскрываются скобки:, т.к. по условию AB=Ф, то

В соответствии с (15):

Далее используются (10а), (26) и (10b) и раскрываются скобки:

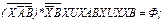
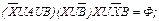
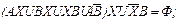
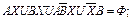
Проводится группировка:

Используются соотношения (9а) и (8а):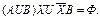

Отсюда записывается решение: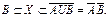

Дата добавления: 2017-01-13