Дизъюнктивная и конъюнктивная нормальные формы

Аналитическое представление логических функций.

Практическая работа N1

Варианты заданий к выполнению работы

Контрольные вопросы

Задания к выполнению работы

Задание1. Определить число внутренний устойчивости графа, заданного в Приложении.

Задание 2. Определить число внешний устойчивости графа, заданного в Приложении.

Задание 3. Определить цикломатическое число и число остовов графа.

Задание 4. Построить матрицу фундаментальных циклов.

Задание 5. Определить компоненты сильной связности, 'провести раскраску графа.

Задание 6. Сравнить результаты, полученные в п.п. 3-5.

Определение графа по № варианта

По номеру ij из таблиц 1-9 Приложения берется таблица с № i; по j из таблицы 10 выбирается строка и осуществляется множества {а, b, с, d, e, f, g, h} столбцов матрицы смежности с № i на цифры из {1, 2, 3, 4, 5, 6, 7, 8} в соответствии с таблицей 10, затем производится перестановка столбцов матрицы смежности в порядке возрастания номеров. В результате получается матрица смежности требуемого графа.

Таблица 2
	a	b	c	d	e	f	g	h

Таблица 1
	a	b	c	d	e	f	g	h

Таблица 3
	a	b	c	d	e	f	g	h

Таблица 4
	a	b	c	d	e	f	g	h

Таблица 6
	a	b	c	d	e	f	g	h

Таблица 5
	a	b	c	d	e	f	g	h

Таблица 8
	a	b	c	d	e	f	g	h

Таблица 7
	a	b	c	d	e	f	g	h

Таблица 10
№	a	b	c	d	e	f	g	h
	Таблица 7 a b c d e f g h

Таблица 9
	a	b	c	d	e	f	g	h

Таблица 1
	a	b	c	d	e	f	g	h

Аналитическое представление предполагает запись произвольной логической функции (ЛФ) в виде формул, переменными в которых являются известные ЛФ.

Дизъюнктивная нормальная форма(ДНФ) – это ЛФ, представляющая собой дизъюнкцию отдельных термов, каждый из которых есть некоторая ЛФ,

содержащая только конъюнкции и инверсии.

Например: F(A,B,C) =

Конъюнктивная нормальная форма (КНФ) - это ЛФ, предоставляющая собой конъюнкцию отдельных термов, каждый из которых есть ЛФ, содержащая только дизъюнктивную и инверсии.

Например: F (A,B,C)= ()().

Для однозначного представления ЛФ используются совершенные дизъюнктивная и конъюнктивная нормальные формы (СДНФ и СКНФ).

СДНФ - это дизъюнктивная форма, в которую входят конъюнкции только максимальные для данной ЛФ ранга.

Например, для функции трех переменных F(A,B,C) совершенной ДНФ будет представление:

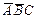F(A,B,C)= v v v v .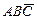

Где каждая элементарная конъюнкция содержит три буквы.

Аналогично определяется СКНФ.

При получении нормальных форм ЛФ, а также при переходе от нормальных форм к совершенным формам обычно пользуются:

1) известными свойствами элементарных функций И, ИЛИ, НЕ

x v x = x; x v 1 = 1; x v 0 = x; ;

x * x = x; x * 1 = x; x * 0 = 0; .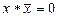

2) законами:

ассоциативным (сочетательным):

x₁ (x₂x₃) = (x₁x₂)x₃ ,

x₁ v (x₂ v x₃) = (x₁ v x₂) v x₃ ;

коммутативным (переместительным):

x₁x₂ = x₂x₁

x₁ v x₂ = x₂ v x₁ ;

дистрибутивным (распределительным):

x₁(x₂ v x₃) = (x₁x₂) v(x₁x3),

x₁ v (x₂x₃) = (x₁ v x₂) v(x₁ v x₃);

де Моргана:

,

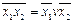склеивания и поглощения:

v x₁x₂ = x₁,

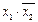() v x₂ = x₁ v x₂.

Пример:

Упростить функцию в ДНФ:

F(x₁,x₂,x₃) = .

Прежде всего, необходимо перевести эту функцию в СДНФ, т.к. только СДНФ дает единственное представление ЛФ, для чего воспользуемся свойствами дизъюнкции и конъюнкции.

x v x = 1; x * 1 = x; x v 1 = 1.

Две последних конъюнкции домножаем на () и (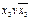) и приводим подобные члены:

F(x₁,x₂,x₃) = =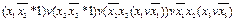

= =

= =

= .

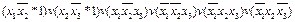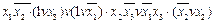Задачи:

1. Упростить ЛФ четырех переменных:

F(x₁,x₂,x₃,x₄) = .

2. Доказать, что F₁(x₁,x₂,x₃) = F₂(x₁,x₂,x₃), если

F₁(x₁,x₂,x₃) = ;

F₂(x₁,x₂,x₃) = x₁ v x₂.

3. Преобразовать в СДНФ и СКНФ следующие функции, представление в ДНФ и КНФ:

а) F₁(x₁,x₂,x₃) = ;

б) F₁(x₁,x₂,x₃) = .

4. Представление ЛФ в ДНФ и КНФ:

а) F₁(x₁,x₂,x₃) = ;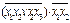

б) F₁(x₁,x₂,x₃ ) = .

5. Упростить ЛФ, используя свойства элементарных функций:

а) F₁(x₁,x₂,x₃) = ;

б) F₁(x₁,x₂,x₃) = v₁(1,2,3,4,5,6,7).

Дата добавления: 2017-01-13