Методы минимизации логических функций

Практическая работа №2

Логические функции небольшого числа переменных (n £ 3) можно минимизировать, используя тождества алгебры логики и законы алгебры логики.

При увеличении числа переменных (n < 6) можно использовать метод карт Карно.

1) Метод карт Карно

Алгоритм метода заключается в следующем:

а) объединяются клетки, составляющие полные квадраты из 4-х или 16-ти клеток;

б) объединяются клетки, составляющие полные столбцы или ряды из 2-х, 4-х или 8-ми клеток, а также 2 рядом расположенных столбца или ряда из 4-х, 16-ти или 8-ми клеток;

в) объединяются 2 соседние клетки в столбце или ряду.

В каждое объединение должно входить максимальное число клеток, одна клетка может входить в несколько объединений.

Если объединить клетки, незанятые, можно получить минимальную ДНФ (МДНФ) для инверсии функции F. Применив к F еще инверсию и закон де Моргана, можно получить минимальную КНФ (МКНФ).

Пример:

Минимизировать функцию

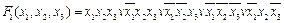
Карта Карно имеет вид:

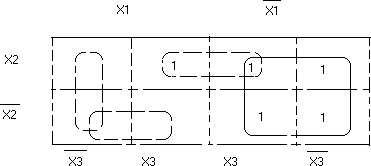
Получаем F₁(x₁,x₂,x₃) = .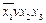

Объединяя клетки, не занятые 1, получаем МДНФ для инверсии функции

.

Инвертируя это выражение и применяя закон де Моргана, получаем МКНФ:

.

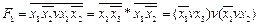При большом числе переменных для минимизации ЛФ можно использовать метод Квайна-Мак-Класки или метод декомпозиции.

2) Метод декомпозиции

Он заключается в выделении более простых составляющих ЛФ и минимизации их по картам Карно, при этом

,

где функции F₁ и F₂ получаются из F путем подстановки в нее

значений x₁=0 для x₁=1 для F₂.

Например,

F = =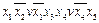

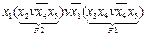
3) Минимизация ЛФ в базисе И-НЕ

Алгоритм метода состоит в следующем:

а) получить МДНФ;

б) произвести двойную инверсию над полученной МДНФ;

в) преобразовать по теореме де Моргана инверсию дизъюнкции в конъюнкцию инверсий по формуле .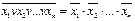

В результате получается ЛФ, содержащая только операции И-НЕ.

Например, пусть имеется МДНФ:

.

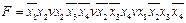Производится двойная инверсия

=

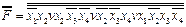и применяется закон де Моргана

= .

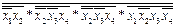4) Минимизация ЛФ в базисе ИЛИ-НЕ

Алгоритм метода состоит в следующем:

а) получить МДНФ;

б) произвести двойную инверсию конъюнкций в дизъюнкцию

инверсий;

в) преобразовать инверсию конъюнкций в дизъюнкцию инверсий:

.

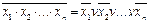В полученной ЛФ содержатся только операции ИЛИ-НЕ.

Например:

.

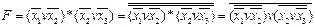5) Минимизация ЛФ в базисе И - ИЛИ – НЕ

Алгоритм:

а) получить МДНФ для инверсии заданной ЛФ по картам Карно;

б) произвести инверсию полученной МДНФ:

Например,

;

.

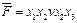Среди алгоритмов минимизации ЛФ от большого числа переменных, легко реализующихся на ЭВМ, наиболее распространен метод Квайна-Мак-Класки.

Задачи:

1. Минимизировать следующие ЛФ четырех с помощью карт Карно:

а) F = v₁(0,2,5,7,8,10,15);

б) F = v₁(1,3,4,5,6,7,10,11);

в) F = v₁(0,2,7,8,13,15);

г) F = v₁(0,2,3,4,5,7,13,15);

д) F = v₁(0,3,5,7,8,11,12,15);

е) F = v₁(5,6,7,9,10,11,14);

ж) F = v₁(0,5,8,11,13,14,15);

з) F = v₁(0,1,2,8,9,10,12,13,14,15).

2. Найти МДНФ методом Квайна-Мак-Класки:

а) F = v₁(0,1,2,3,4,5,6,10,12,13,14);

б) F = v₁(0,1,2,6,7,9,11,14,15).

3. Минимизировать с помощью карт Карно ЛФ:

F = 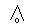(1,2,3,4,6,7,10,11,12,14).

4. Представить МДНФ, найденные в задаче 1, в базисах И-НЕ, ИЛИ-НЕ.

Литература

1) В.А. Горбатов. "Основы дискретной математики". М.: Высшая школа, 1986.

2) О.П. Кузнецов, Г.М. Адельсон-Вельский. "Дискретная математика для инженера", М.: Энерготомиздат, 1988.

3) Лекции по теории графов / Емелигев В.А. и др. - М.: Наука, 1990

Дата добавления: 2017-01-13