Неупорядоченные наборы элементов из данных без повторений

Неупорядоченные наборы 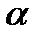элементовиз данных без повторений будем просто называть набором. (Иногда называют сочетанием 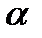элементов из данных).

Пример: {123} наборы двух элементов из 3: {12} {13} {23}. Наборы из данных это 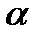-элементные подмножества -элементного

множества.

Теорема. Число -элементных наборов есть Обозначают это чи­сло

Доказательство. Рассмотрим все упорядоченные наборы 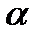элементов из без повторений и разобьем их на группы так, что в одну груп­пу попадают упорядоченные наборы, состоящие из одних элементов множества , (т.е. в группе, в которой содержится упорядо­ченный набор , содержатся все перестановки элементов ), и поэтому число упорядоченных наборов в каждой

группе есть .значит число групп есть , а это число групп и есть число 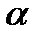-элементных подмножеств множества и по­этому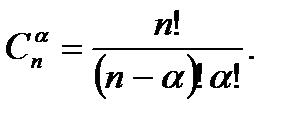

Пример 1. Каким числом способов можно создать группу из 10 человек

на курсе из 100 человек.

Решение. Очевидно, что искомое число есть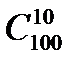

Пример 2. Бином Ньютона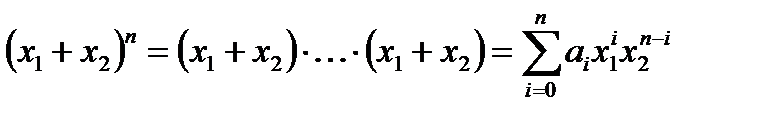

Коэффициент 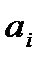, равен числу наборов i элементов из п данных (числу вы­боров i скобок из n данных, в которых для образования слагаемого брали , а в невыбранных скобках брали 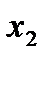), и поэтому =

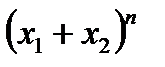Как частный случай получим очевидное равенство .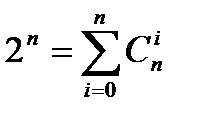

Пример 3. Графом без петель называют множество вершин V= и множество некоторых пар вершин Е: называе­мых ребрами, здесь петлей называют пару , (и таких пар в Е нет). Полным графом на множестве вершин V= называют граф со всеми ребрами, т.е. Е есть все пары из множества кроме петель.

Из теоремы следует, что число ребер в полном графе есть

Дата добавления: 2017-01-13