Основы теории перечисления Пойа. Лемма Бернсайда

Пример. Какое число ожерелий из 3-х бусин можно составить из бусин 2-х

цветов: красного (к) и синего (с).

Решение. Здесь два ожерелья неотличимы, если одно из другого мож­но получить преобразованием вращения или, как называют, циклической перестановкой на множестве 3-х элементов из множества {к, с}.

Например, ожерелье к с с эквивалентно ожерелью с к с, так как второе можно получить из первого при циклической перестановке, когда первый элемент переходит на второе ме­сто, второй на третье, а третий на первое. Рассмотрим все циклические перестановки трех элементов G:

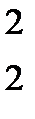
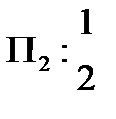
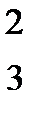
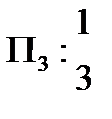
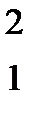
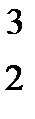
Первая перестановка – тождественная; вторая-вращение против часовой стрелки, когда первый элемент переходит на второе место, второй, на третье, третий на первое; третья-вращение по часовой стрелке. Рассмотрим все слова из алфавита 0-к, 1-с длинны три:

000, 001, 010, 011, 100, 101, 110, 111

Некоторые из рассматриваемых ожерелий, как мы выяснили, эквивалентны, т.е. все множество ожерелий разбивается на классы эквивалентных ожерелий: любая пара ожерелий в одном классе эквивалентна между собой, а пара из разных - неэквивалентна. Поэтому число классов и есть требуемое число.

Чтобы получить класс, в котором лежит некоторое ожерелье, например 001, нужно к нему применить все перестановки G. В данном случае

001 .

Общее разбиение ожерелий имеет вид:

{000}{001, 100, 010}{011, 101, 110}{111}.

Т.е. число различных ожерелий равно 4.

В задачах такого рода имеется множество объектов (всевозможные слова алфавита {к, с}); множество преобразований одного объекта в другой, что означает неотличимость объектов (все циклические перестановки трех элементов).

Тогда множество преобразований будет разбивать множество объектов на классы эквивалентных объектов.

Утверждение 1. Множество преобразований, нами рассматриваемое, будет группой перестановок (т.е. каждое преобразование слова заключается в перестановке его букв).

Дадим строгое определение группы перестановок.

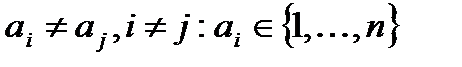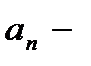Перестановкой слова , называют преобразованием слова длинны n, при котором первая буква переходит на ое место, вторая на ое место, ая на ое.

Например, (2 1 4 3) (к с к к)=с к к к.

Произведением двух перестановок называют преобразование, полученное в результате последовательного применения преобразования 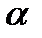, потом преобразования .

Утверждение 2. Произведение перестановок является перестановкой.

Пример. (2 1 4 3) (3 2 4 1)=(2 3 1 4).

Утверждение 3. Произведение перестановок обладает свойством ассоциативности:

Определим место, на которое перейдет s -ый элемент от перестановки в левой и правой частях равенства

,

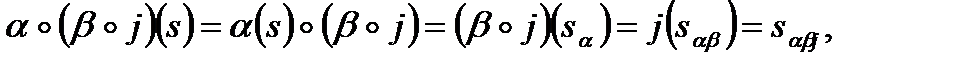
т.е. один и тот же элемент.

Тождественной или единичной перестановкой e называют перестановку, оставляющую все буквы на месте (1 2 n).

Утверждение 4. перестановки .

Обратной к перестановке называют перестановку , такую что .

Утверждение 5. Обратная к любой 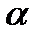существует единственна, и .

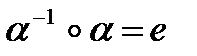Доказательство. Докажем утверждение на примере. Пусть 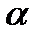:(2 4 3 1).

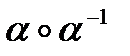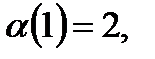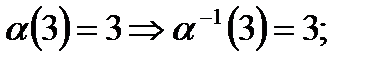
При преобразовании каждый элемент должен остаться на своем месте. значит т. е. (4 1 3 2).

Множество элементов с бинарной, ассоциативной операцией , единичным элементом e и обратным 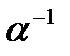для каждого 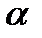называется группой.

Подгруппой группы называют подмножество элементов группы, которое само является группой.

Утверждение 6. Чтобы подмножество конечной группы являлась группой необходимо и достаточно, чтобы оно было замкнуто относительно групповой операции

Доказательство. Необходимость очевидна.

Достаточность: Пусть множество замкнутое относительно операции . Возьмем произвольный элемент 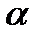и будем брать степени

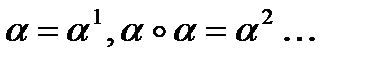до тех пор пока не получим элемент который был в этом ряду ранее: Тогда и если не единица, т.е. k 2, то есть обратный к . Т.е. подмножество есть группа.

Дата добавления: 2017-01-13