Основы метода производящих функций

Упражнения.

1. Имеется колода карт четырех мастей по n карт каждой масти. Берут 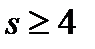карт. Найти число комбинаций, в которых имеются все масти.

2. Бросают различных игральных кубиков. Найти число комбина­ций, когда имеются все цифры.

3. Найти число квадратных двоичных матриц размера n n, в каждой строке которых содержится хотя бы один ноль.

4. Найти число двоичных матриц размера n в строках, кото­рых содержатся все двоичные слова длины m.

5. Составляют n -значные числа из цифр 1,2,3,4. Найти число чисел, в

которых имеются все цифры.

Пусть имеется некоторая последовательность целых положительных чисел: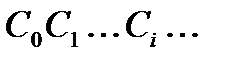

Производящей функцией последовательности 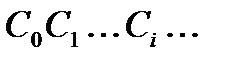называют формальный ряд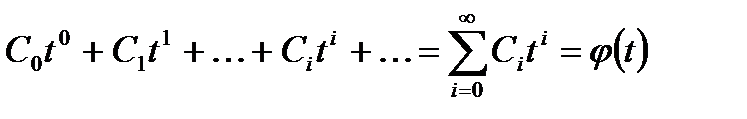

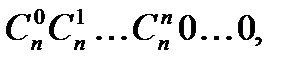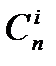Пример 1. Рассмотрим последовательность где — число неупорядоченных наборов без повторений i элементов из n имеющихся. Тогда

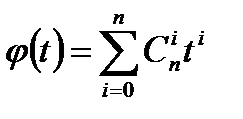
но, с другой стороны, рассмотрим функцию 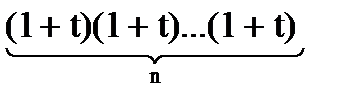и рас-

кроем в ней скобки, тогда коэффициент при есть число выборов i скобок из n имеющихся, в которых брали t, а в остальных1. Таким образом, =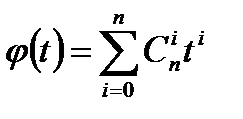

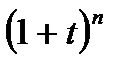
Тогда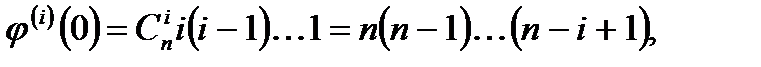

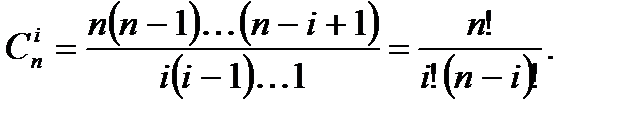
Пример 2. Производящая функция последовательности неупорядочен­ных наборов с повторениями 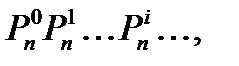где — число неупорядо­ченных наборов с возможными повторениями i элементов из п имеющихся,

Но, с другой стороны, рассмотрим функцию

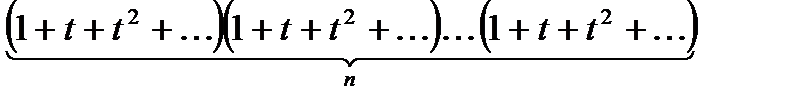и раскроем в ней скобки, тогда коэффициент при равен числу решений уравнения

в целых числах, что и является числом . Поэтому

=

Пример 3. Производящая функция последовательности неупорядочен­ных наборов i элементов из n данных, где только первый элемент может повториться 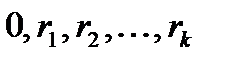раз .

В частности производящая функция последовательности неупорядочен­ных наборов, где только первый элемент может повторяться, есть

= .

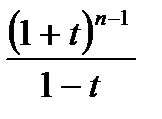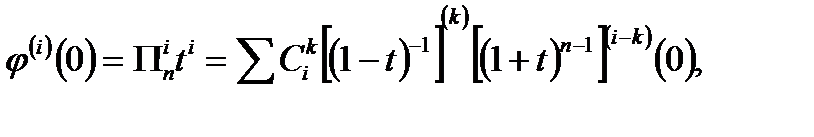
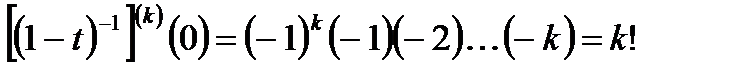
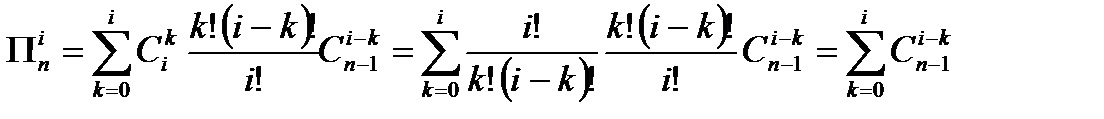
Здесь во второй строке применена формула Лейбница для производной про­изведения.

Пример 4. Производящая функция последовательности перестановок из n элементов 1,2,... ,п с определенным числом инверсий

Вектором инверсий перестановки 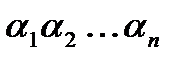называют n -компонентный вектор, где i -ая его компонента равна числу чисел больших i, стоящих левее i в перестановке .

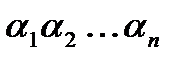1324 0100.

Утверждение 1. Вектор инверсии, т.е. вектор целых чисел, i -ая компо­нента. которого принимает значения 0,1,..., п — i, однозначно определяет перестановку.

Однозначность видна из примера выше: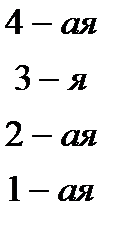

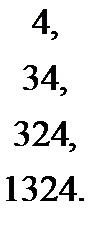
Поэтому число перестановок с i инверсиями — это число инверсных векто­ров с суммой компонент = i: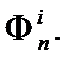

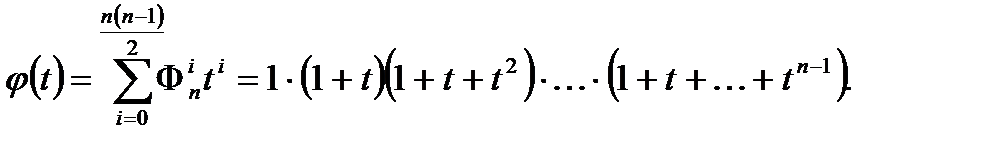
Дата добавления: 2017-01-13