
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лінійні однорідні рівняння з постійними коефіцієнтами
|
|
|
|
Задача знаходження фундаментальної системи рішень, а отже й загального рішення, спрощується у випадку рівняння з постійними коефіцієнтами.
Означення. Рівняння виду y 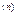 +a
+a  y
y 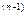 +…+a
+…+a  y=0, де а
y=0, де а  ,…,а
,…,а  – довільні константи, називається лінійним однорідним рівнянням з постійними коефіцієнтами.
– довільні константи, називається лінійним однорідним рівнянням з постійними коефіцієнтами.
Рішення рівняння шукають у вигляді у=  . Підставляючи у=
. Підставляючи у=  у рівняння отримаємо, що k задовольняє рівнянню kⁿ+a
у рівняння отримаємо, що k задовольняє рівнянню kⁿ+a  k
k 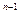 +…+a
+…+a  =0.
=0.
Означення. Рівняння kⁿ+a  k
k 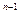 +…+a
+…+a 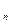 =0 називають характеристичним рівнянням для даного диференціального рівняння.
=0 називають характеристичним рівнянням для даного диференціального рівняння.
Існує декілька випадків відносно розв’язка характеристичного рівняння.
1. Характеристичне рівняння має n різних дійсних коренів  . Розглянемо функції у
. Розглянемо функції у  =
= 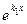 ,…, у
,…, у 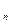 =
=  усі вони є рішеннями даного диференціального рівняння і лінійно незалежні, оскільки
усі вони є рішеннями даного диференціального рівняння і лінійно незалежні, оскільки
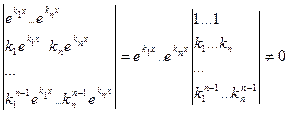 .
.
Отже у  =
= 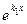 ,…, у
,…, у 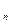 =
=  - фундаментальна система рішень і у=с
- фундаментальна система рішень і у=с 
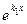 +…+с
+…+с 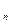
 – загальне рішення лінійного однорідного диференціального рівняння з постійними коефіцієнтами.
– загальне рішення лінійного однорідного диференціального рівняння з постійними коефіцієнтами.
2. Припустимо, що якийсь корінь ki дійсний, але має кратність p. Тоді  – лінійно незалежна система функцій, які також являються рішеннями вихідного рівняння, що не важко перевірити підставляючи їх у рівняння, враховуючи кратність ki. Загальний розв’язок рівняння будується аналогічно 1 з урахуванням вище сказаного.
– лінійно незалежна система функцій, які також являються рішеннями вихідного рівняння, що не важко перевірити підставляючи їх у рівняння, враховуючи кратність ki. Загальний розв’язок рівняння будується аналогічно 1 з урахуванням вище сказаного.
3. Припустимо, щохарактеристичне рівняння має комплексний корінь k  =α+βi, тоді спряжене число k
=α+βi, тоді спряжене число k 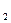 =α-βi теж корінь характеристичного рівняння. Цім кореням відповідають дві функції
=α-βi теж корінь характеристичного рівняння. Цім кореням відповідають дві функції 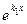 ,
, 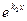 в фундаментальній системі розв’язків.
в фундаментальній системі розв’язків.
Скористувавшись формулами Ейлера ці функції можна замінити на дійснозначні. Оскільки
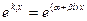 = (cosβx+isinβx)
= (cosβx+isinβx) 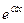 ,
, 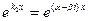 = (cosβx-isinβx)
= (cosβx-isinβx) 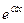 , то
, то  ,
,
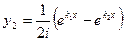 , або у
, або у  = cosβx
= cosβx 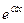 , у
, у 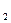 =sinβx
=sinβx 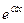 – рішення рівняння і лінійно незалежні. Загальний розв’язок будується аналогічно 1.
– рішення рівняння і лінійно незалежні. Загальний розв’язок будується аналогічно 1.
4. Якщо комплексний корінь k  =α+βi має кратність p, спряжений корінь k
=α+βi має кратність p, спряжений корінь k 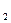 =α-βi теж має кратність p. Тоді аналогічно випадкам 2 і 3 цім кореням відповідає система лінійно незалежних рішень рівняння:
=α-βi теж має кратність p. Тоді аналогічно випадкам 2 і 3 цім кореням відповідає система лінійно незалежних рішень рівняння:
cosβx 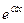 , xcosβx
, xcosβx 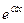 ,…,
,…, 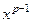 cosβx
cosβx 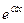 , sinβx
, sinβx 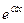 ,xsinβx
,xsinβx 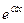 ,…,
,…, 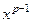 sinβx
sinβx 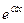 , за допомогою яких і будується загальне рішення.
, за допомогою яких і будується загальне рішення.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 663; Нарушение авторских прав?; Мы поможем в написании вашей работы!