
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дискретная математика 2 страница
|
|
|
|
f. линейным (или полным), если 
Теорема 4.3.1. Пусть 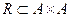 – отношение на
– отношение на 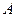 . Тогда:
. Тогда:
1)  рефлексивно тогда и только тогда, (далее используется знак Û) когда
рефлексивно тогда и только тогда, (далее используется знак Û) когда  .
.
2)  симметрично Û
симметрично Û  .
.
3)  транзитивно Û
транзитивно Û 
4)  антисимметрично Û
антисимметрично Û  .
.
5)  антирефлексивно Û
антирефлексивно Û  Æ.
Æ.
6)  полно Û
полно Û 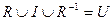 .
.
§5. Функции
Определение 5.1. Свойство отношения 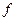 из
из 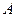 в
в  такое, что
такое, что
 называется однозначностью (или функциональностью). Само отношение
называется однозначностью (или функциональностью). Само отношение 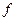 называется функцией из
называется функцией из 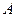 в
в  .
.
Обозначение:  или
или 
Замечание 5.1.: всякому отношению  из
из 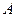 в
в  можно поставить в соответствие функцию
можно поставить в соответствие функцию  , полагая
, полагая  (такая функция называется характеристической).
(такая функция называется характеристической).
Определение 5.2. Пусть  , тогда множество
, тогда множество 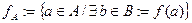 называется областью определения функции, а
называется областью определения функции, а  - областью значений функции.
- областью значений функции.
Определение 5.3. Если  , то функция называется тотальной. В противном случае
, то функция называется тотальной. В противном случае 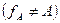 – частичной. Сужением функции
– частичной. Сужением функции  на множестве
на множестве  называется функция, определяемая (и обозначаемая) следующим образом:
называется функция, определяемая (и обозначаемая) следующим образом:

Замечание 5.2.: для тотальной функции  .
.
Определение 5.4. Функция  называется функцией
называется функцией 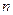 - аргументов (или
- аргументов (или 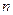 - местной функцией).
- местной функцией).
Определение 5.5. Функция  называется:
называется:
а) инъективной (или инъекцией),
если  ;
;
б) сюръективной (или сюръекцией),
если 
в) биективной (или биекцией), если она инъективна и сюръективна.
Определение 5.6. Пусть  и
и  .
.
Множество 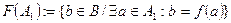 называется образом множества
называется образом множества  .
.
Множество  .
.
Замечание 5.3.:  является отношением из множества
является отношением из множества  во множество
во множество  :
:
 &
&  &
& 
§6. Отношения эквивалентности
Определение 6.1. Рефлексивное, симметричное и транзитивное отношение называется отношением эквивалентности.
Обозначение: º
Определение 6.2. Пусть º - отношение эквивалентности на множестве 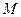 и пусть
и пусть  . Подмножество множества
. Подмножество множества 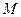 , состоящее из элементов, эквивалентных
, состоящее из элементов, эквивалентных 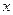 , называется классом эквивалентности для
, называется классом эквивалентности для 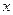 :
:
Обозначение:  &
& 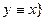
Теорема 6.1. Всякое отношение эквивалентности на множестве 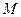 определяет разбиение этого множества, причем среди элементов разбиения нет пустых. Обратное также верно: всякое разбиение множества
определяет разбиение этого множества, причем среди элементов разбиения нет пустых. Обратное также верно: всякое разбиение множества 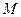 , не содержащее пустых элементов, определяет отношение эквивалентности на множестве
, не содержащее пустых элементов, определяет отношение эквивалентности на множестве 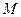 .
.
Определение 6.3. Если  – отношение эквивалентности на множестве
– отношение эквивалентности на множестве 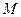 , то множество классов эквивалентности называется фактор - множеством множества
, то множество классов эквивалентности называется фактор - множеством множества 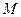 по эквивалентности
по эквивалентности  .
.
Обозначение: 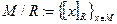
Замечание 6.1.: Фактор – множество является подмножеством булеана, т.е.
 .
.
§7. Отношения порядка
Определение 7.1. Антисимметричное, транзитивное отношение называется отношением порядка. Если отношение порядка является рефлексивным, то оно называется отношением нестрогого порядка. Если же отношение порядка является антирефлексивным, то оно называется отношением строгого порядка.
Определение 7.2. Если отношение порядка является полным, то оно называется отношением полного порядка. Если отношение порядка не обладает свойством полноты, то оно называется отношением частичного порядка.
Обозначение: < - отношение строгого порядка, £ - отношение нестрогого порядка.
Определение 7.3. Множество, на котором определено отношение частичного порядка, называется частично упорядоченным. Множество, на котором определено отношение полного порядка, называется вполне упорядоченным.
Пример 7.1. Множество действительных чисел вполне упорядоченно. Булеан – частично упорядоченное множество.
Определение 7.4. Элемент 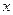 множества
множества 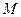 с отношением порядка называется минимальным, если не существует элементов, меньших
с отношением порядка называется минимальным, если не существует элементов, меньших 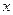 :
:
 &
& 
Пример 7.2. Пустое множество Æ является минимальным элементом булеана по включению.
Теорема 7.1. Во всяком конечном, непустом, частично упорядоченном множестве существует минимальный элемент.
Замечание 7.1. Вполне упорядоченное конечное множество содержит один минимальный элемент. Конечное частично упорядоченное множество может иметь несколько минимальных элементов.
Определение 7.5. Пусть 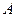 и
и  – упорядоченные множества и
– упорядоченные множества и  . Если
. Если  , то функция называется монотонной, а если
, то функция называется монотонной, а если  , то функция
, то функция  называется строго монотонной.
называется строго монотонной.
Определение 7.6. Пусть  и
и  - отношения на множестве
- отношения на множестве 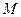 . Отношение
. Отношение  называется замыканием отношения
называется замыканием отношения  относительно свойства
относительно свойства  , если выполняются условия:
, если выполняются условия:
1.  обладает свойством
обладает свойством 
2.  является надмножеством
является надмножеством 
3.  является наименьшим:
является наименьшим:  &
& 
Глава 2. Булевы функции
§1. Элементарные булевы функции. Основные понятия.
Определение 1.1 :булевой (логической) переменной называется переменная, принимающая лишь два значения “  ” и “
” и “  ”.
”.
Определение 1.2 :булевой функцией от 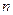 логических переменных называется функция, принимающая также лишь два значения “
логических переменных называется функция, принимающая также лишь два значения “  ” и “
” и “  ”.
”.
Из определения логической функции следует, что функция 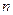 переменных - это отображение из
переменных - это отображение из 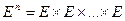 (декартово произведение множества
(декартово произведение множества  самого на себя
самого на себя 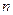 раз) в
раз) в  . Это отображение можно задать непосредственно таблицей, которая называется таблицей истинности данной функции.
. Это отображение можно задать непосредственно таблицей, которая называется таблицей истинности данной функции.
Например, функция трех переменных f(x,y,z) может определяться следующей таблицей истинности:
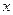
| 
| 
| 
|
Это означает, что f (0,0,0)=1, f (0,0,1)=0, f (0,1,0)=1 и т.д.
Все функции 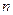 переменных можно перенумеровать. Число таких функций равно
переменных можно перенумеровать. Число таких функций равно  .Однако, некоторые из них являются по существу функциями меньшего числа переменных, а две - вообще константами.
.Однако, некоторые из них являются по существу функциями меньшего числа переменных, а две - вообще константами.
Определение 1.3: Если функция не зависит от некоторой переменной, то такую переменную будем называть фиктивной (несущественной).
§ 2. Булевы функции одной переменной
| Переменная x | ||||
| Название | Обозначение | Фиктивные | ||
| нуль | ||||
| тождественная | x | |||
| отрицание | x, 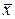 , , 
| |||
| единица |
§3.Булевы функции двух переменных
Переменная 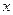
| ||||||
Переменная 
| ||||||
| Название | Обозначение | Фиктивные | ||||
| нуль | 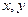
| |||||
| конъюнкция | ·, &, 
| |||||

| ||||||
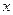
| ||||||
| сложение по модулю 2 | +, 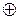 , , 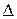
| |||||
| дизъюнкция | 
| |||||
| стрелка Пирса | 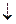
| |||||
| эквивалентность | ~, 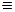
| |||||
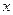
| ||||||

| ||||||
| импликация |  , ,  , , 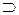
| |||||
| штрих Шеффера | | | |||||
| единица | 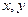
|
§ 4. Свойства конъюнкции, дизъюнкции и отрицания
Эти функции принято считать основными. Определение этих функций легко может быть перенесено на любое число переменных.
Определение 4.1: Конъюнкцией 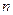 переменных
переменных  называется функция, которая принимает значение 1, тогда и только тогда, когда все переменные равны 1 (и, значит, равна 0, если хотя бы одна из этих переменных равна 0).
называется функция, которая принимает значение 1, тогда и только тогда, когда все переменные равны 1 (и, значит, равна 0, если хотя бы одна из этих переменных равна 0).
Определение 4.2: Дизъюнкцией 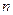 переменных
переменных  называется такая функция, которая равна 0 тогда и только тогда, когда все переменные равны 0 (и, значит, равна 1, когда хотя бы одна из этих переменных равна 1).
называется такая функция, которая равна 0 тогда и только тогда, когда все переменные равны 0 (и, значит, равна 1, когда хотя бы одна из этих переменных равна 1).
Будем обозначать через  новую функцию, которая на наборе переменных x 1, x 2, …, xn принимает значение, противоположное f(x 1, x2,…, xn).
новую функцию, которая на наборе переменных x 1, x 2, …, xn принимает значение, противоположное f(x 1, x2,…, xn).
Основные свойства этих функций:
1) Идемпотентность.
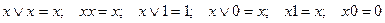
2) Ассоциативность конъюнкции и дизъюнкции.

3) Поглощение (“Целое поглощает часть”):

4) Распределительные законы:

5) Закон двойного отрицания

6) 
7) Правила де Моргана: 

Эти правила обобщаются на любое число переменных:
 ;
; 
§ 5. ДНФ, СДНФ, КНФ, СКНФ
Определение 5.1: Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная (либо сама, либо ее отрицание) встречается не более одного раза.
Например,  является простой конъюнкцией.
является простой конъюнкцией.
Определение 5.2: Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение  является ДНФ.
является ДНФ.
Определение 5.3: Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.
Например, выражение  является ДНФ, но не СДНФ. Выражение
является ДНФ, но не СДНФ. Выражение
 является СДНФ.
является СДНФ.
Определение 5.4: Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная (либо сама, либо ее отрицание) входит в дизъюнкцию не более одного раза.
Например, выражение  является простой дизъюнкцией.
является простой дизъюнкцией.
Определение 5.5: Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций.
Например, выражение  является КНФ.
является КНФ.
Определение 5.6: Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания) причем в одном и том же порядке.
Например, выражение  является СКНФ.
является СКНФ.
§ 6. Представление логических функций в виде СДНФ (СКНФ)
Теорема 6.1. Всякая булева функция (кроме 0) имеет единственную СДНФ.
Следствие. Всякая булева функция может быть выражена через дизъюнкцию, конъюнкцию и отрицание. В частности, 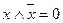 .
.
Теорема 6.2. Всякая булева функция (кроме 1) может быть единственным образом представлена в виде СКНФ.
Алгоритм построения СДНФ булевой функции по заданной таблице истинности:
берем только те наборы переменных 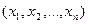 , для которых
, для которых  и составляем простую конъюнкцию для этого набора так: если
и составляем простую конъюнкцию для этого набора так: если  , то берем в этой конъюнкции
, то берем в этой конъюнкции  , если
, если  , то берем
, то берем  . Составляя дизъюнкцию этих простых конъюнкций, мы придем к СДНФ.
. Составляя дизъюнкцию этих простых конъюнкций, мы придем к СДНФ.
По аналогии с представлением любой функции (не равной 0) в виде СДНФ можно любую функцию (не равную 1), представить в виде СКНФ. А именно, простые дизъюнкции составляются для тех наборов переменных 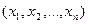 , для которых
, для которых 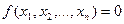 , причем если в наборе
, причем если в наборе  , то в простую дизъюнкцию включаем
, то в простую дизъюнкцию включаем  , если же
, если же  , то в неё включаем -
, то в неё включаем -  .
.
Пример 6.1. Составим СДНФ и СКНФ для импликации и сложения по модулю 2.
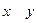
| 
| 
|
| 0 0 | 1 | |
| 0 1 | 1 | |
| 1 0 | 0 | 1 |
| 1 1 | 1 | 0 |
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 458; Нарушение авторских прав?; Мы поможем в написании вашей работы!