Дискретная математика 3 страница

СДНФ для этих функций имеет вид:

СКНФ для этих функций будет иметь вид:

§ 7. Полином Жегалкина

Определение 7.1: Полиномом (многочленом) Жегалкина от 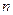переменных называется функция вида

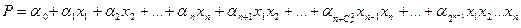
Всего здесь слагаемых, коэффициенты являются константами (равными нулю или единице), “+” означает сложение по модулю 2, каждый одночлен представляет собой конъюнкцию входящих в него переменных и констант.

Теорема 7.1. Любая булева функция 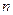переменных может быть единственным образом представлена полиномом Жегалкина.

Способы построения полинома Жегалкина:

А) Пусть логическая функция задана своей таблицей истинности. Представляем нашу функцию в виде полинома Жегалкина с неопределенными коэффициентами. По очереди подставляем всевозможные наборы переменных и находим коэффициенты полинома из получающихся уравнений. Так как число наборов равно числу коэффициентов (и равно ), то последние определяются однозначно.

Б) Этот способ основан на том, что 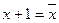и применяется для функций, заданных в виде ДНФ. А именно, если функция задана в виде ДНФ, то сначала убираем дизъюнкцию, используя одно из правил де Моргана, а все отрицания заменяем сложением по модулю 2 с единицей. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно нулю (так как ), а нечетное число одинаковых слагаемых равно одному такому слагаемому.

Пример 7.1:

Последнее выражение и есть полином Жегалкина данной функции.

Глава 3. Комбинаторика

§ 1. Основные понятия

Комбинаторика – раздел математики, посвящённый способам подсчёта числа элементов в конечных множествах. Она изучает количества комбинаций, подчиненных определённым условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества.

Основными задачами комбинаторики являются:

а) определение типа комбинации;

б) подсчёт количества комбинаций.

Основные принципы комбинаторики

Дата добавления: 2017-01-13