Реализация графа G

.

Матрица инцидентности графа G.

3 4

Замечание. В матрице B сумма элементов i строки равна deg v_i.

Пусть G – любой (n, m) граф. Упорядочим множество его вершин VG={v_1, v_2, ¼, v_n} и ребер EG={e_1, e₂, ¼, e_m}. Определим теперь матрицу инцидентности A, полагая

Пример 2.2. Определить матрицу инциденций для графа G.

Рассмотрим теперь произвольный (n,m)-орграф G=(V,D). Упорядочим множество его вершин V={v_1, v_2, v_{3, …,} v_n} и ребер D={f_1, f_{2, …,} f_m}. Определим его матрицу инцидентности

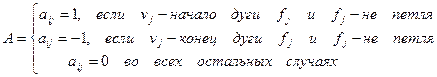
Пример 2.3. Определить матрицу инцидентности для графа G.

Для наглядности граф часто представляют в виде геометрического объекта: вершинам соответствуют различные выделенные точки в пространстве (на плоскости), ребрам – отрезки кривых, связывающие соответствующие точки и не проходящие через выделенные точки, отличные от их концов. Отношению инцидентности вершин и ребер графа соответствует при этом геометрическая инцидентность выделенных точек и линий. Кроме того, предполагается, что кривые попарно не пересекаются во внутренних точках. Такое представление графа называется его реализацией.

Пример 2.4. Дан ориентированный граф с множеством вершин V={1,2,3,4,5,6,7}, который задан списком дуг E={(1,4), (1,6), (2,1), (2,2), (2,6), (2,6), (3,2), (3,4), (4,6), (5,2), (5,4), (5,4), (5,5), (6,2), (6,5), (7,1), (7,6)}. Построить реализацию графа G.

Решение: Изображения вершин 1,2,3,4,5,6.7 удобно поместить в вершинах правильного семиугольника. Соединить пары вершин в соответствии со списком дуг, избегая пересечения трех ребер в одной точке. Обозначить стрелками ориентацию дуг.

§ 3. Маршруты, цепи, циклы, связность

1) Пусть G – неориентированный граф.

Определение 3.1. Маршрутом в графе G называется чередующаяся последовательность вершин и ребер , в которой 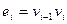_, . Такой маршрут кратко называют маршрутом. Вершины – концевые вершины маршрута.

Определение 3.2. Если , то называется замкнутым.

Определение 3.3. Цепью называется маршрут без повторяющихся ребер.

Определение 3.4. Цепь называется простой или элементарной, если в ней нет повторяющихся вершин, кроме, быть может, совпадающих концевых вершин.

Определение 3.5. Замкнутая простая цепь называется циклом.

Замечание 3.1. Цикл полностью определяется множеством своих ребер, поэтому часто под циклом мы будем понимать соответствующее ему множество ребер. Петля дает цикл длины 1, пара кратных ребер образует цикл длины 2.

Определение 3.6. Граф G называется связным, если для любых двух различных его вершин существует маршрут (т.е. две любые его вершины связаны цепью).

Утверждение 3.1. Вершины называются связными тогда и только тогда, когда существует маршрут.

Легко видеть, что отношение связности является отношением эквивалентности. Обозначим через V₁, V₂, …,V_k классы этого отношения. Пусть G_i = G(V_i) – подграф, порожденный множеством вершин V_i. Тогда графы G_1, G₂,…, G_k называются компонентами связности графа G. Ясно, что любая компонента связности является связным подграфом. Очевидно, что любой связный подграф графа G является подграфом некоторой его компоненты связности. Поэтому множество компонент связности – это множество всех максимальных связных подграфов данного графа, и любое ребро принадлежит некоторой компоненте связности.

Для любого графа G есть две возможности: либо ребро e содержится в некотором цикле графа, либо e не содержится ни в каком цикле графа. В первом случае ребро называется циклическим ребром, а во втором – ациклическим.

§ 4. Леса, деревья, остовы, цикломатическое число

Определение 4.1. Лесом называется ациклический граф.

Определение 4.2. Деревом называется связный ациклический граф.

Замечание 4.1. Очевидно, что лес не содержит петель и кратных ребер.

Пусть G – связный граф. Если G содержит хотя бы один цикл, то, удаляя из графа G некоторое ребро этого цикла, мы уменьшим число циклов, по крайней мере, на 1, сохранив связность графа. Ясно, что, последовательно разрушая циклы данного графа, можно прийти к остовному подграфу, являющемуся деревом. Такой подграф называется остовным деревом связного графа G. Т. к. дерево с n вершинами содержит n-1 ребер, то для получения остовного дерева из графа G нужно удалить m-n+1 ребер. Если G – произвольный граф, то объединение остовных деревьев его компонент связности приводит к остовному лесу или остову графа G. Поскольку лес с 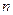вершинами и компонентами связности содержит ребер, то для получения остова из графа G нужно удалить m-n+k ребер.

Определение 4.3. Число называется цикломатическим числом.

Замечание. При подсчёте не учитываются петли и кратные рёбра.

Пример 4.1. Неориентированный граф с множеством вершин V={1, 2, 3, 4, 5, 6, 7} задан списком ребер E={(1,2), (1,4), (1 6), (1,7), (2,3), (2,5), (2,6), (3,4), (3,6), (4,5), (4,6), (5,6), (5,7)}.

1) Построить реализацию графа.

2) Найти цикломатическое число графа.

3) Выбрать остов графа.

Решение:

1. Построим реализацию графа G (смотри пример 2.4)

2. Найдем цикломатическое число графа G по формуле , где m - число ребер, n - число вершин, k - число компонент связности графа (m=13, n=7, k=1). Следовательно, .

3. Выбираем остов графа G. Поскольку число вершин графа G равно 7, то в любом его остове должно быть 6 ребер. При заданном упорядочении вершин 1-7, начиная с вершины 1, последовательно добавляем ребра, присоединяющие к строящемуся дереву новую вершину: (1,2), (1,4), (1,6), (1,7), (2,3), (2,5).

СОДЕРЖАНИЕ

1. Глава 1. Теория множеств и отношений………………………………3

2. Глава 2. Булевы функции……………………………………………… 9

3. Глава 3. Комбинаторика………………………………………………..14

4. Глава 4. Элементы теории графов……………………………………..19

Дата добавления: 2017-01-13