Числовые характеристики статистического распределения

Средней арифметической вариационного ряда называется сумма произведений всех вариант на соответствующие частоты, деленная на сумму частот:

,

где х_i - варианты дискретного ряда или середины интервалов непрерывного ряда распределения;

n_i – частоты вариант в вариационном ряду.

Средняя величина дает общую характеристику усредняемого признака, но не показывает, насколько она типична для данной совокупности. Показатели вариации (изменения, колебаний) позволяют измерить изменение величины количественного признака от одного объекта исследуемой совокупности к другому.

Размах вариации - это разность между максимальным и минимальным значениями признака

где R - размах вариации;

х_max - максимальное значение признака;

х_min - минимальное значение признака.

Следует отметить, что размах вариации весьма неустойчив и поэтому может служить лишь для грубой оценки.

Выборочная дисперсия Dв характеризует рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения. Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонений вариант от их среднего арифметического значения :

Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

Пример 14. Вычислить числовые характеристики (среднее арифметическое, выборочную дисперсию и выборочное среднее квадратическое отклонение) данного интервального ряда распределения.

Данные о сроке и количестве осужденных и лишению свободы.

таблица 5

Срок лишения свободы (в годах)	2-3	3-6	6-8	8-10	10-15
Количество осужденных (чел.)
Накопленная частота

Преобразуем интервальный ряд в дискретный. Для этого найдем среднее значение срока лишения свободы в каждом интервале, что составит:

Дальнейшее вычисление проводится по формуле для подсчета средней арифметической.

года

Вычислим значение выборочной дисперсии и выборочного среднего квадратического отклонения.

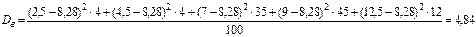
Дата добавления: 2017-01-13