Парная линейная корреляция

Функциональная и корреляционная зависимости.

Математические основы анализа и прогнозирования социально-правовых процессов.

Изучение разнообразных явлений сопровождается выяснением закономерностей, которым подчиняются характерные для данных явлений количественные соотношения или связи. Различают два типа связей: функциональную и статистическую.

Функциональной зависимостью некоторой величины Y от нескольких переменных х₁, х₂,…, х_n называется связь, в соответствии с которой Y зависит только от перечисленных переменных х₁, х₂,…, х_n и каждому значению переменных х₁, х₂,…, х_n соответствует только одно значение Y.

Понятия функции недостаточно, чтобы описать всевозможные причинные связи, с которыми жизнь нас сталкивает повседневно. В реальном мире все явления и процессы связаны между собой, и нет такого конечного числа переменных х₁, х₂,…, х_n, которые абсолютно полно определяли бы собою случайную величину Y, в силу чего функциональная зависимость является абстракцией, упрощающей действительность. Например, совершенно очевидно, что между ростом и весом человека существует зависимость, но мы знаем сколько угодно людей, у которых одинаковый рост, но разный вес. Следовательно, зависимость веса от роста не является функциональной.

Статистической зависимостью величины Y от нескольких переменных х₁, х₂,…, х_n называется связь, в соответствии с которой при изменении значения факторных переменных х₁, х₂,…, х_n результативная переменная Y может принимать любые значения с некоторыми вероятностями, но ее среднее значение или иные статистические характеристики изменяются по определенному закону. Статистическая связь между различными показателями предполагает, что каждый из них имеет случайную вариацию индивидуальных значений относительно средней величины.

Корреляционной связью двух переменных X и Y называют частный случай статистической связи, состоящий в том, что разным значениям факторной переменной X соответствуют различные средние значения результативной переменной Y.

Простейшей системой корреляционной связи является линейная связь между двумя признаками - парная линейная корреляция. Подобные системы встречаются в тех случаях, когда среди всех действующих факторов выделяется один важнейший, который и определяет вариацию результативного признака, а нелинейные формы связей без особого ущерба могут быть преобразованы в линейные.

Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид:

,

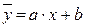где – среднее значение результативного признака Y при определенном значении факторного признака X;

b – свободный член уравнения;

а – коэффициент регрессии, характеризующий вариацию Y, приходящуюся на единицу вариации X.

Коэффициенты уравнения регрессии рассчитываются по методу наименьших квадратов.

Параметр “a” определяется из соотношения

,

где – среднее значение случайной величины x×y;

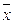и 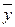– средние значения факторного и результативного признаков соответственно;

s_x – среднее квадратичное отклонение признака X;

x_i и y_i - индивидуальные значения соответствующих признаков.

Параметр b выражают из уравнения регрессии и вычисляют, подставляя средние значения признаков X и Y и найденное значение параметра а:

.

При парной связи ее теснота измеряется с помощью коэффициента корреляции:

Соотношение между значением коэффициента корреляции и теснотой связи представлено в таблице 6.

таблица 6

Значение модуля коэффициента корреляции	Характер связи
0,00 – 0,30	крайне слабая или отсутствует
0,30 – 0,50	слабая
0,50 – 0,70	средняя
0,70 – 0,99	сильная

Рассматривая возможные значения коэффициента корреляции, следует учитывать, что нулевая величина этого коэффициента соответствует полному отсутствию какой-либо связи. Это возможно при полном взаимном погашении положительных и отрицательных отклонений признаков от их средних величин. Поскольку вероятность этого крайне мала для любой реальной совокупности, кроме бесконечно большой, то коэффициент корреляции для реальной совокупности отличен от нуля и при отсутствии связи!

Значение коэффициента корреляции, равное 1 (или -1) соответствует функциональной связи. Чем ближе связь к функциональной, тем ближе абсолютная величина коэффициента корреляции к единице. Отрицательное значение коэффициента корреляции свидетельствует об обратной зависимости.

Пример 15. Определение корреляции между затратами на содержание органа внутренних дел и уровнем преступности на обслуживаемой территории (табл.2).

Таблица 2.

№	Затраты руб./тыс. населе­ния, х	Уровень преступности на тыс. населения, у		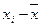	(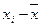)* ()	()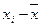^2	()^2	Расчетные значения уровня преступности
1.			1,75	-8,81	-15,42	3,06	77,66
2.			-844	209,2	-176606,55	712758,06	43759,41
3.			-560	65,19	-36521,30	313880,06	4249,41
4.			153,8	7,188	1105,08	23639,06	51,66
5.			-2,25	0,188	-0,42	5,06	0,04
6.			-492	13,19	-6491,55	242310,06	173,91
7.			-376	25,19	-9476,80	141564,06	634,41
8.			-262	5,188	-1360,42	68775,06	26,91
9.			29,75	74,19	2207,08	885,06	5503,79
10.			143,8	-64,8	-9316,80	20664,06	4200,66
11.			127,8	-36,8	-4702,80	16320,06	1355,16
12.			129,8	-27,8	-3608,67	16835,06	773,54
13.			53,75	-37,8	-2032,42	2889,06	1429,79
14.			5,75	5,188	29,83	33,06	26,91
15.			951,8	-108	-102610,55	905828,06	11623,54
16.			939,8	-121	-113533,55	883130,06	14595,66
å					-462935,25	3349519,0	88482,44

Задание 1.

Тема. Случайные величины.

Цель. Нахождение решений математических задач из теории дискретных случайных величин с помощью табличного процессора Excel.

Задача 1.1. По мишени производится 15 выстрелов. Построить ряд распределения случайной величины – числа попаданий в мишень, если вероятность попадания при каждом выстреле равна 0,4. Найти числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение этой случайной величины.

Задача 1.2. На экспертизу взяли 50 одинаковых купюр, из которых 15 –фальшивые. Для проверки отобраны случайным образом 10 купюр. С помощью текстового процессора Excel постройте ряд распределения случайной величины X – числа фальшивых купюр в выборке. Найдите числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение этой случайной величины.

Задача 1.3. Следователь проводит допрос. Вероятность того, что первый подозреваемый даст необходимую информацию равна 0,6, второй - 0,3. С помощью текстового процессора Excel постройте ряд распределения случайной величины X – числа подозреваемых, давших необходимую информацию. Найдите числовые характеристики: математическое ожидание, дисперсию, среднеквадратическое отклонение этой случайной величины.

Дата добавления: 2017-01-13