Оценка точности вычисления «неберущихся» интегралов

В данной работе вычисление абсолютной и относительной погрешности проводится при условии, что известно точное значение определенного интеграла. Однако не всякая первообразная, даже тогда, когда она существует, выражается в конечном виде через элементарные функции. Таковы первообразные, выраженные интегралами 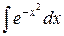, , , 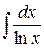и т.д. Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций.

Определенные интегралы от таких функций можно вычислить только приближенно. Для оценки точности вычисления в таких случаях используют, например, правило Рунге. В данном случае интеграл вычисляется по выбранной формуле (прямоугольников, трапеций, парабол Симпсона) при числе шагов, равном n, а затем при числе шагов, равном . Погрешность вычисления значения интеграла при числе шагов, равном , вычисляется по формуле Рунге: , для формул прямоугольников и трапеций , а для формулы Симпсона . Таким образом, интеграл вычисляется для последовательных значений числа шагов , ,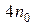..., где – начальное число шагов. Процесс вычислений заканчивается, когда для очередного значения будет выполнено условие , где – заданная точность.

Для того чтобы не вычислять один и тот же интеграл по нескольку раз для разных разбиений отрезка интегрирования, можно вычислить шаг интегрирования заранее.

Пример. Выбрать шаг интегрирования для вычисления интеграла с точностью 0,01 пользуясь квадратурными формулами прямоугольников, трапеций, Симпсона.

Квадратурная формула прямоугольников.

Вычислим, при каком шаге 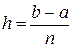погрешность будет составлять 0,01:

.

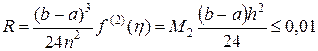Поскольку 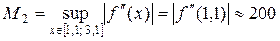, то

.

При шаге отрезок разбивается на равностоящих узлов.

Квадратурная формула трапеций.

Вычислим, при каком шаге 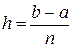погрешность составит 0,01:

.

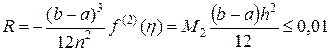Поскольку , .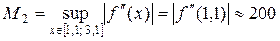

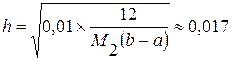При шаге ,отрезок разбивается на равностоящих узлов.

Квадратурная формула Симпсона.

Вычислим, при каком шаге 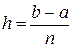погрешность составит 0,01:

,

, .

При шаге , отрезок разбивается на равностоящих узлов.

Как и следовало ожидать, наименьшее количество равностоящих узлов получается при вычислении интеграла по квадратурной формуле Симпсона.

Содержание РГР «Приближенные методы вычисления

определенных интегралов»

Студенту предлагается работа, состоящая из четырех этапов:

1 этап – точное вычисление определенного интеграла.

2 этап – приближенное вычисление определенного интеграла одним из методов: прямоугольников или трапеций.

3 этап – приближенное вычисление определенного интеграла методом парабол.

4 этап – расчет и сравнение абсолютной и относительной ошибок приближенных методов: 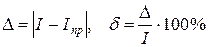, где – точное решение интеграла, 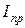– значение интеграла, полученное с помощью приближенных методов.

Построение графика подынтегральной функции.

Варианты и образец выполнения РГР приведены ниже.

Варианты

№ варианта	f (x)	a	b	Шаг h
			π/2	0,05π
				0,1
				0,1
				0,1
			π/2	0,05π
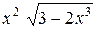
				0,1
			π/2	0,05π
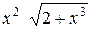
				0,1
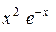
				0,1
				0,1
				0,1
				0,1
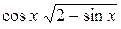
			π/2	0,05π
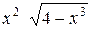
				0,1
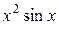
				0,1
				0,1
			π/2	0,05π
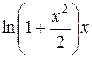
				0,1
				0,1
				0,1
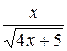
				0,1
			π/2	0,05π
				0,1
			π/2	0,05π
				0,1
			π/2	0,05π
				0,1
			π/2	0,05π
				0,1
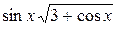
			π	0,1π

Дата добавления: 2017-01-13