Образец выполнения РГР

Задание. Вычислить интеграл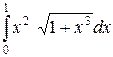

1. Точное вычисление:

= 0,40631714.

2. Приближенное вычисление с помощью формул прямоугольников:

,

, .

, .

Составим таблицу:

№	xi	yi = f (xi)
	0,1	0,010005
	0,2	0,04016
	0,3	0,091207
	0,4	0,165041
	0,5	0,265165
	0,6	0,396981
	0,7	0,567851
	0,8	0,786966
	0,9	1,065081
		1,414214

По первой формуле прямоугольников получаем:

≈ 0,1 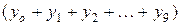= 0,1·3,062514 = 0,306251.

По второй формуле прямоугольников получаем:

≈ 0,1 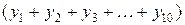= 0,1· 4,802669 = 0,480267.

В данном случае первая формула дает значение интеграла с недостатком, вторая – с избытком.

Вычислим относительную и абсолютную погрешности.

I = 0,40631714, , ,

, .

, .

3. Приближенное вычисление по формуле трапеций:

В нашем случае получаем:

≈ 0,1 = =0,1 = 0,1·4,095562 = =0,409556.

Вычислим относительную и абсолютную погрешности.

I = 0,40631714, ,

, .

4. Приближенное вычисление по формуле Симпсона:

В нашем случае получаем:

≈ =

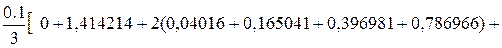
= = 0,406325.

Вычислим относительную и абсолютную погрешности.

I = 0,40631714, ,

, .

В действительности, = 0,40631714.

Таким образом, при разбиении отрезка на 10 частей по формуле Симпсона мы получили 5 верных знаков; по формуле трапеций – три верных знака; по формуле прямоугольников мы можем ручаться только за первый знак.

Литература:

1. Задачи и упражнения по математическому анализу для втузов: учеб. пособие для втузов / Г. С. Бараненков [и др.]; под ред. Б.П. Демидовича. - М.; Владимир: Астрель: Изд-во АСТ: ВКТ, 2010. – 495 с.

2. Кудрявцев, Л.Д. Краткий курс математического анализа: учеб. для вузов. Т. 1: Дифференциальное и интегральное исчисления функций одной переменной. Ряды / Л. Д. Кудрявцев. - 3-е изд., перераб. - М.: ФИЗМАТЛИТ, 2009. – 399 с.

3. Пискунов, Н.С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов. В 2 т. Т. 1 / Н. С. Пискунов. - Изд. стер. - М.: Интеграл-Пресс, 2004. – 415 с.

4. Письменный, Д.Т. Конспект лекций по высшей математике: полн. курс / Д.Т. Письменный. – 9-е изд. – М.: Айрис-пресс, 2009. – 608 с.

Баранова И.М., Часова Н.А.

МАТЕМАТИКА

ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ

ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

Методические указания к выполнению расчетно-графической работы для студентов всех специальностей и всех направлений подготовки бакалавров очной формы обучения

Формат Объем Тираж Заказ

Брянск, Станке Димитрова 3, Редакционно-издательский отдел

Отпечатано: Печатный цех БГИТУ

Дата добавления: 2017-01-13