
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гаусс теоремасы 2 страница
|
|
|
|
 (2.2)
(2.2)
Потенциалды (консервативті) күшке ауырлық күшін, электр зарядтарының өзара әсерлесу күшін, серіппенің серпімділік күшін жатқызуға болады.
Денелер жүйесінің механикалық энергиясы
Механикалық энергияның екі түрі бар: кинетикалық 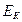 және потенциалдық
және потенциалдық  . Олардың қосындысы жүйедегі толық механикалық энергияны Е береді.
. Олардың қосындысы жүйедегі толық механикалық энергияны Е береді.
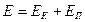 . (2.3)
. (2.3)
Механикалық жүйенің кинетикалық энергиясы 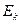 :
:
 . (2.4)
. (2.4)
Потенциалдық энергия – жүйе бөлшектерінің өзара орналасуы мен олардың сыртқы күш өрістерінде орналасуына байланысты болатын жүйенің механикалық энергиясының бір түрі.
1) массасы 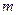 болатын
болатын  биіктікке көтерілген дененің потенциалдық энергиясы
биіктікке көтерілген дененің потенциалдық энергиясы
 ; (2.5)
; (2.5)
2)  шамасына керілген серіппенің потенциалдық энергиясы
шамасына керілген серіппенің потенциалдық энергиясы
 ; (2.6)
; (2.6)
3) Бір-бірінен 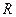 қашықтықта орналасқан массалары m1 және m2 болатын денелердің өзара әсерлесуі кезіндегі потенциалдық энергиясы
қашықтықта орналасқан массалары m1 және m2 болатын денелердің өзара әсерлесуі кезіндегі потенциалдық энергиясы
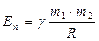 ; (2.7)
; (2.7)
4)Бір-бірінен 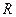 қашықтықта орналасқан зарядталған q1 және q2 зарядтары бар екі дененің бір-біріне әсері кезіндегі потенциалдық энергия
қашықтықта орналасқан зарядталған q1 және q2 зарядтары бар екі дененің бір-біріне әсері кезіндегі потенциалдық энергия
 . (2.8)
. (2.8)
Механикалық энергияның сақталу заңы
Консервативті жүйедегі толық механикалық энергия уақыт бойынша өзгермейді.
 . (2.9)
. (2.9)
Жүйенің энергиясы бір түрден екінші түрге өтіп, жүйе бөлшектерінің арасына бөлінеді бірақ, жүйенің толық энергиясының өзгерісі барлық процесте де осы жүйеге сырттан алынған энергияға тең болады.
Қуат уақыт бірлігінде жасалатын жұмысқа тең шама:
N=dA/dt. (2.9)
Күш моменті
Дене айналу үшін оған түсірілетін күш оське байланысты момент тудыруы қажет.  күшінің моменті деп қозғалмайтын О (3.2-сур.) нүктесіне қатысты векторды айтамыз.
күшінің моменті деп қозғалмайтын О (3.2-сур.) нүктесіне қатысты векторды айтамыз.
 , (2.10)
, (2.10)
мұндағы  - күштің түсірілу нүктесінің радиус-векторы.
- күштің түсірілу нүктесінің радиус-векторы.  векторы О нүктесі арқылы өтеді.
векторы О нүктесі арқылы өтеді.
Дененің инерция моменті
Дененің инерция моменті - дененің айналу кезіндегі инерттілігін сипаттайтын шама.
Материялық нүктенің  инерция моменті айналу осі бойынша нүкте массасының
инерция моменті айналу осі бойынша нүкте массасының 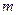 нүктеден осы оське дейінгі
нүктеден осы оське дейінгі 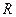 арақашықтығының квадратына көбейтіндісіне тең:
арақашықтығының квадратына көбейтіндісіне тең:
 . (2.11)
. (2.11)
Дененің инерция моменті айналу осіне байланысты оның барлық материялық нүктелерінің инерция моменттерінің қосындысына тең:
 . (2.12)
. (2.12)
Айналмалы қозғалыс кезіндегі дененің инерттілігіне дене пішіні мен геометриялық өлшемі, айналу осінен қандай қашықтықта орналасуы, массаның көлемдік орналасуы әсер етеді.
2.1 - кестеде кейбір денелердің инерция моменттері келтірілген.
2.1- кесте
| Дене | Айналу осінің орналасуы | Инерция моменті |
| Қуыс жұқа қабырғалы радиусы R цилиндр | Симметрия осі | 
|
Радиусы 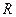 тұтас цилиндр немесе дискі тұтас цилиндр немесе дискі
| Симметрия осі | 
|
Ұзындығы  жіңішке стержень жіңішке стержень
| Ось стерженнің ортасы арқылы өтеді және оған перпендикуляр. | 
|
Радиусы 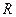 тұтас шар тұтас шар
| Симметрия осьі | 
|
Егер айналу осі дененің масса центрі арқылы өтпейтін болса, оның инерция моменті Штейнертеоремасы арқылы анықталады:
 2.3-сурет. Біртекті жіңішке стержень
2.3-сурет. Біртекті жіңішке стержень
|
 . (2.13)
. (2.13)
Мысалы, біртекті жіңішке ұзындығы  массасы
массасы 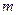 стерженнің инерция моменті (2.3-сур.)
стерженнің инерция моменті (2.3-сур.)  осьіне қатысты мынаған тең:
осьіне қатысты мынаған тең:

Импульс моменті және оның сақталу заңы
Массасы 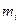 қатты дененің кішкентай бөлшегін қарастырайық. Оның жылдамдығы
қатты дененің кішкентай бөлшегін қарастырайық. Оның жылдамдығы 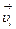 және оған қатысты импульсі
және оған қатысты импульсі  нүкте траекториясына жанама бойымен бағытталған.
нүкте траекториясына жанама бойымен бағытталған.
 2.4-сурет. Импульс моментін анықтау
2.4-сурет. Импульс моментін анықтау
| Қозғалмайтын О нүктесіне қатысты импульс моменті векторы  материялық нүктенің радиус-векторы материялық нүктенің радиус-векторы  мен оның импульсінің мен оның импульсінің  векторлық көбейтіндісіне тең физикалық шама: векторлық көбейтіндісіне тең физикалық шама:
 . (2.14)
Импульс моменті векторы . (2.14)
Импульс моменті векторы  векторлық көбейтінді ережесі арқылы анықталып, айналу осі бойында жатады, ал оның модулі мына өрнекпен анықталады: векторлық көбейтінді ережесі арқылы анықталып, айналу осі бойында жатады, ал оның модулі мына өрнекпен анықталады:
 (2.15) (2.15)
|
Қатты дененің айналмалы қозғалыс динамикасының негізгі теңдеуі
 немесе
немесе  . (2.16)
. (2.16)
Өзін-өзі бақылауға арналған тесттер:
1. Массасы m = 2 кг материалдық нүкте тұрақты күш әсерінен x = Bt + Ct2 + Dt3 теңдеуіне сәйкес түзу сызықты қозғалады. Мұндағы В = -2 м/с, C = 1 м/с2, D = -0,2 м/с3 . Қозғалыстың t1 = 2 с және t2 = 5 с мезеттерінде нүкте өндіретін қуатты табу керек.
A) 0,32 Вт, 96Вт
B) 35,2 Вт, -396Вт
C) 3,52 Вт, -196Вт
D) 32 Вт, -19Вт
E)2 Вт, 6Вт
2. Бөлшек xy жазықтығында F = 3 i + 4 j күш әсерінен радиус - векторы r1 = 1 i + 2 j 1 нүктеден радиус-векторы r2 = 2 i -3 j 2 нүктеге белгілі бір траекториямен орын ауыстырды. F күшінің осы орын ауыстыруда істеген жұмысын табу керек.
A) 33 Дж
B) 23 Дж
C) 29 Дж
D) 53 Дж
E) 44 Дж
3. Массасы 4 кг денені 5 м биіктікке көтергендегі жұмысты анықтау керек.
A) 200 Дж
B) 300 Дж
C) 250 Дж
D) 20 Дж
E)280 Дж
4. Ұзындығы l = 1 м жеңіл созылмаймын жіпке ілінген шарикті түртіп, оған υ = 6 м/с жылдамдық береді. Жіптің босаңсып, ал шарик шеңбер бойымен қозғалуын қоятын биіктікті табу керек. Осы мезеттегі шарик жылдамдығы неге тең?
A) 1 м, 5 м/с
B) 1 м, 3 м/с
C) 1,0 м, 1 м/с
D) 1,8 м, 0 м/с
E)1,8 м, 4,4 м/с.
5. Массасы 1 кг денені горизонтқа 30о бұрыш жасатын көлбеу жазықтық бойымен жоғары жібереді. Дененің бастапқы жылдамдығы 10 м/с және үйкеліс коэффиценті 0,2. Дененің толық тоқтағанға дейін жүрген жолын тап.
A) 3 м/с
B) 12 м/с
C) 4,4 м/с.
E) 6,7 м/с.
e)7,5 м.
6.Массасы m нейтрон тыныштықта тұрған көміртегі атомымен соқтығысады (mс = 12 m). Соқтығысуды орталық және серпімді деп есептеп, нейтрон жылдамдығының 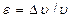 қандай бөлігі жоғалтатынын табу керек.
қандай бөлігі жоғалтатынын табу керек.
A) 5/9
B) 4/13
C) 2/9
D) 6/11
E)7/9
3-дәріс
Тұтас орталар механикасың элементтері. Бернулли теңдеуі. Стокс формуласы. Пуазейл өрнегі. Тұтас орта түсінігі. Идеал және тұтқыр сұйықтық. Арнайы салыстырмалылық теориясының элементтері. Эйнштейн постулаттары. Жылдамдықтарды қосудың релятивистік заңы. Импульс пен энергияны релятивистік түрлендіру.
Тұтас орта механикасының элементтері
Гидродинамика – сұйық орта қозғалыстарының заңдылықтарын және оның денелермен әрекеттесуін зерттейтін механиканың бір саласы.
Сұйық сығылмайды деп есептесек, онда бұл көлемдер бір-біріне тең:
 (3.1)
(3.1)
Осы өрнекті ағынның үздіксіздік теңдеуі деп атайды. Ағын түтігі көлденең қимасының сұйық ағысының жылдамдығына көбейтіндісі тұрақты шама.
Бернулли теңдеуі
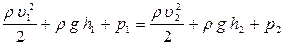 , (3.2)
, (3.2)
Қималарды ток түтікшесінің кез-келген нүктесінен алуға болатындықтан соңғы теңдеуді мына түрде жазуға болады:
 (3.3)
(3.3)
Ағын түтігі горизонталь орналасса Бернулли теңдеуі ( ):
):
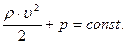 (3.4)
(3.4)
Сұйықтық горизонталь аққан кезде үйкеліс болмаса динамикалық және статикалық қысымының қосындысы ток түтікшесі қимасының барлық нүктелерінде бірдей болады.
 , (3.5)
, (3.5)
Және ағын жылдамдығын алуға болады.
 . (3.6)
. (3.6)
Онда тесіктен аққан сұйықтықтың жылдамдығын Торричелли өрнегі деп атайды:
 . (3.7)
. (3.7)
Тұтқырлық
Тұтқырлық депнақты сұйықтықтардың қабаттар арасында ішкі үйкеліс құбылысының пайда болуы айтылады. Ньютонның зерттеулері бойынша бұл күштің шамасы мынадай өрнекпен анықталады:
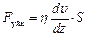 , (3.8)
, (3.8)
мұндағы  –жылдамдық градиенті, ол
–жылдамдық градиенті, ол 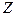 осьі бағытында бір қабаттан екіншісіне өткен кезде жылдамдық қалай тез өзгеретінін көрсетеді;
осьі бағытында бір қабаттан екіншісіне өткен кезде жылдамдық қалай тез өзгеретінін көрсетеді; 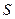 – жанасатын қабаттардыңбетінің ауданы;
– жанасатын қабаттардыңбетінің ауданы;  – динамикалықтұтқырлық коэффициенті. Ішкі үйкеліс күшінің шамасы қабаттарының беттесу ауданына және жылдамдықтың градиентіне пропорционал.
– динамикалықтұтқырлық коэффициенті. Ішкі үйкеліс күшінің шамасы қабаттарының беттесу ауданына және жылдамдықтың градиентіне пропорционал.
Сұйықтық ағынының екі түрі
Сұйықтықтың ағысы ламинарлық және турбуленттік деп екіге бөлінеді. Сұйықтықтың жеке қабаттары бір-біріне қарағанда параллель, яғни сұйық қабатта бірі-бірімен араласпай қозғалатын болса, онда ол ағыс ламинарлық деп аталады.
Түтік бойымен сұйық ағысы кезіндегі ағыстың бір түрінен екінші түрге көшу шарты Рейнольдс саны деп аталатын шамамен анықталады.
 , (3.9)
, (3.9)
мұндағы:  – кинематикалық тұтқырлық,
– кинематикалық тұтқырлық,  – сұйықтықтың тығыздығы,
– сұйықтықтың тығыздығы, 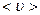 – орташа ағыс жылдамдығы,
– орташа ағыс жылдамдығы,  – түтік диаметрі. Егер ішкі үйкеліс күші және ағыс жылдамдығы аз болса, онда қозғалысты ламинарлық деп қарастыруға болады. Турбуленттік ағысқа өту үшін Рейнольдс саны мына аралықта болуы керек
– түтік диаметрі. Егер ішкі үйкеліс күші және ағыс жылдамдығы аз болса, онда қозғалысты ламинарлық деп қарастыруға болады. Турбуленттік ағысқа өту үшін Рейнольдс саны мына аралықта болуы керек  .
. 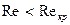 кезінде ағыс ламинарлық болады. Тұтқырлықтың әсерінен
кезінде ағыс ламинарлық болады. Тұтқырлықтың әсерінен 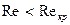 кезінде түтіктің дөңгелек қимасының әртүрлі қабаттардағы ағыс жылдамдықтары әртүрлі болады. Оның орташа мәні Пуазейль өрнегі бойынша анықталады.
кезінде түтіктің дөңгелек қимасының әртүрлі қабаттардағы ағыс жылдамдықтары әртүрлі болады. Оның орташа мәні Пуазейль өрнегі бойынша анықталады.
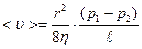 , (3.10)
, (3.10)
мұндағы  -түтік радиусы, (
-түтік радиусы, ( ) –түтік ұштарындағы қысым айырымы,
) –түтік ұштарындағы қысым айырымы,  -оның ұзындығы.
-оның ұзындығы.
Мысалы, Стокс сұйықтықта қозғалған радиусы r, жылдамдығы  шарға әсер ететін күші үшін келесі өрнекті анықтады:
шарға әсер ететін күші үшін келесі өрнекті анықтады:
 , (3.11)
, (3.11)
r – шар радиусы,  - оның қозғалыс жылдамдығы. Бұл өрнек Стокс теңдеуі деп аталады.
- оның қозғалыс жылдамдығы. Бұл өрнек Стокс теңдеуі деп аталады.
Арнайы салыстырмалы теорияның элементтері
Арнайы салыстырмалылықтың теорияныңнегізін Эйнштейн тұжырымдаған екі постулат құрайды.
1. Табиғаттың барлық заңдары бір инерциалды санақ жүйесінен екінші инерциалды санақ жүйесіне өтуіне қатысты өзгермейді (инвариант болады).
2. Жарықтың вакуумдағы жылдамдығы барлық инерциалды санақ жүйелерінде бірдей және жарық көзі мен қабылдағыштың қозғалу жылдамдығына тәуелсіз.
Бұл постулаттардан төмендегі өте маңызды салдарлар келіп шығады:
1) Ұзындықтың қысқаруы
 ,
,
2) Массаның артуы
 ,
,
3) Уақыттың баяулауы
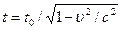 ,
,
4) Жылдамдықтарды қосу ережесі
 ,
,
5) Дененің толық энергиясы
 .
.
Лоренц түрлендірулері мына түрде анықталған:
 ,
,  ,
,  ,
, 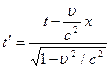 . (3.12)
. (3.12)
Релятивистік динамика элементтері
Импульстің жылдамдыққа тәуелділігі классикалық механикаға қарағанда біршама күрделі екендігі көрінеді.
 . (3.13)
. (3.13)
Өзін-өзі бақылауға арналған тесттер:
1.Массасы  импульсі p 1 болатын 1 бөлшек тыныш тұрған массасы
импульсі p 1 болатын 1 бөлшек тыныш тұрған массасы  болатын 2 бөлшекпен серпімді соқтығысады. Бөлшектердің соқтығысудан кейінгі p 11 және p 12 импульстарын табу керек. Соқтығысудың нәтижесінде 2 бөлшек 1 бөлшектің бастапқы бағытымен
болатын 2 бөлшекпен серпімді соқтығысады. Бөлшектердің соқтығысудан кейінгі p 11 және p 12 импульстарын табу керек. Соқтығысудың нәтижесінде 2 бөлшек 1 бөлшектің бастапқы бағытымен  бұрышпен ауытқиды.
бұрышпен ауытқиды.
A)  ;
; 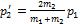
B)  ;
; 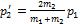
C)  ;
;  .
.
D)  ;
; 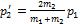
E)  ;
; 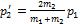
2. Идеал сұйық көлбеу жазықтықпен стационар ағады. Ағын тереңдігі l арақашықтықта екі есе кемиді. Қандай арқашықтықта ағын тереңдігі төрт есе кемиді?
A) 2l
B) 4l
C) 3l
D) 6l
E)5 l.
3. Биік цилиндр ыдыстың түбіндегi саңылаудан су ағады. Ыдыс қимасының ауданы саңылау қимасының ауданынан 100 есе үлкен. Ыдыстағы судың деңгейі араласатын үдеуді табу керек.
A) 10-3 g
B) 9g.
C)  .
.
D) 10-8g
E) 10g
4. Радиусы R = 0,2 м біртекті дискінің жиегіне F = 98,1 H тұрақты жанама күш түсірілген. Айналу кезінде дискіге Мүйк = 4,9 Н∙ м үйкеліс күшінің моменті әсер етеді. Диск тұрақты 100 рад/с  бұрыштық үдеумен айналады. Дискінің массасын анықтау керек.
бұрыштық үдеумен айналады. Дискінің массасын анықтау керек.
A) 
B) 
C) 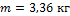
D) 
E) 
5. Қандай жылдамдықта бөлшектің кинетикалық энергиясы оның тыныштық энергиясына тең болады?
A) 1,3 м/с
B)  м/с.
м/с.
C) 4,3 м/с
D) 9,3 м/с
Е)1,6 м/с
4-дәріс
Термодинамикалық параметрлер және процестер. Идеал газ күйінің теңдеуі.
Идеал газдың молекула-кинетикалық теориясы. Статистикалық таралу.
Тасымалдау құбылыстары. Диффузия. Тұтқырлық. Жылу өткізгіштік.
Термодинамикалық параметрлер мен процестер
Жүйенің күйін сипаттау үшін жүйенің термодинамикалық параметрлері (күй параметрлері) деп аталатын физикалық шамалар енгізілген. Оларға р – қысым,  – көлем, Т – температура, п – концентрация және т.б. жатады.
– көлем, Т – температура, п – концентрация және т.б. жатады.
Қысым р – дененің бірлік бетіне нормаль бойымен әсер ететін күшке тең шама  Өлшем бірлігі – Па (Паскаль) (
Өлшем бірлігі – Па (Паскаль) ( ).
).
Жүйенің температурасы – оның бөлшектерінің жылулық қозғалыс қарқынының өлшемі. Физикада бірнеше температуралық шкала қолданылады. Мысалы, Кельвин ( ) және Цельсий (
) және Цельсий ( ) шкалаларындағы температуралар өзара
) шкалаларындағы температуралар өзара
T = t + 273,15 (4.1)
өрнегімен байланысқан.
Қалыпты күйде термодинамикалық параметрлер келесі мәндерге тең болады:
p =1,013· 105 Па, VM =22,4· 10-3 м3, T =273,15 K. (4.2)
Термодинамикалық процесс деп жүйенің кез - келген параметрінің өзгерісін айтады.
Идеал газдың күй теңдеуі
Идеал газдың күй теңдеуі – термодинамикалық параметрлер арасындағы функционалдық байланыс:  :
:
 . (4.3)
. (4.3)
Мұндағы V – газдың молярлық көлемі;  – универсал газ тұрақтысы
– универсал газ тұрақтысы  . Бұл Менделеев – Клапейронтеңдеуі. Бұл теңдеуді тағы бір түрде жазуға болады:
. Бұл Менделеев – Клапейронтеңдеуі. Бұл теңдеуді тағы бір түрде жазуға болады:  немесе
немесе
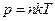 . (4.4)
. (4.4)
Мұндағы:  – мөлшері 1 моль заттағы молекулалар санына тең Авогадро саны,
– мөлшері 1 моль заттағы молекулалар санына тең Авогадро саны,  – Больцман тұрақтысы,
– Больцман тұрақтысы,  – молекулалар концентрациясы (бірлік көлемдегі газ бөлшектерінің саны). Тұрақты температурада газ қысымы молекулалардың концентрациясына пропорционал болады.
– молекулалар концентрациясы (бірлік көлемдегі газ бөлшектерінің саны). Тұрақты температурада газ қысымы молекулалардың концентрациясына пропорционал болады.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 1126; Нарушение авторских прав?; Мы поможем в написании вашей работы!