Список літератури. Cхема до коду Хеммінга

Висновок

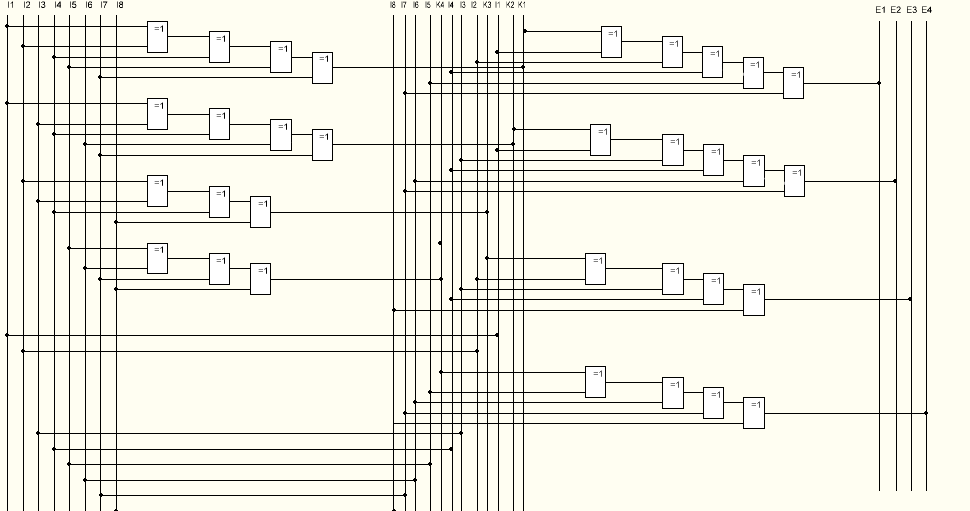
Cхема до коду Хеммінга

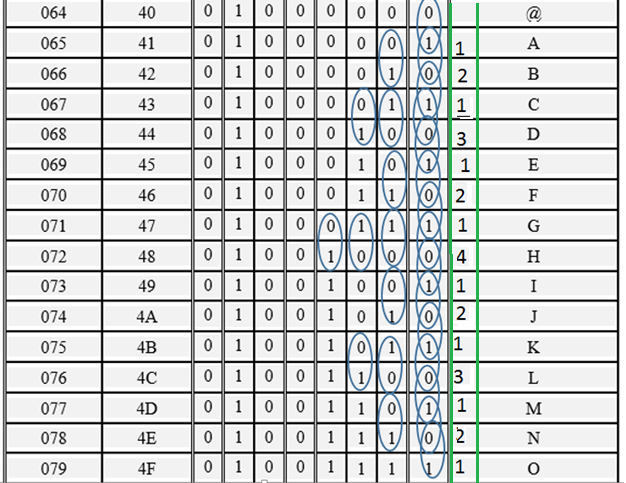
Відстань Хеммінга

Відстань Хеммінга (кодова відстань)— число позицій, у яких відповідні цифри двох двійкових слів однакової довжини різні. У загальнішому випадку відстань Хеммінга застосовується для рядків однакової довжини будь-яких q -кових абеток і служить метрикою відмінності (функцією, що визначає відстань в метричному просторі) об'єктів однакової вимірності.

Одним з найважливіших розділів теорії кодування є завдання кодування чисел, яка знаходиться на межі двох галузей науки: теорії чисел і теорії кодування інформації. Саме таке двояке положення завдання кодування чисел і вимога виконання арифметичних і логічних операцій над числами привело до появи нового розділу математики – теорії систем числення.

З часом в теорії систем числення з'явилися результати, які виходили за рамки її традиційних завдань. Це перш за все можливість реалізації на основі тих або систем числення завдань перетворення кодів, наприклад, питань стискування інформації або завдостійкого кодування. Код є форма представлення повідомлення, не залежна від його фізичної суті. Це відрізняє код від сигналу, який визначає фізичне представлення повідомлення в системі зв'язку. Коди, що дозволяють виявити і виправити помилки в кодових комбінаціях називаються завадостійкими або корегуючими кодами. Вони діляться на дві групи: коди з виявленням помилок і коди з виявленням та виправленням помилок. Введення надмірності в код дозволяє окрім виявлення і виправлення помилок підвищити енергетичну ефективність лінії зв'язку, звузити частотний спектр переданого сигналу, скоротити час входження в зв'язок шляхом підвищення завадозахисного тракту синхронізації, поліпшити кореляційні властивості ансамблю сигналів, простими засобами реалізувати рознесений прийом.

Коди Хеммінга – лінійні коди, які забезпечують виявлення та корекцію помилок. Використовуються при передачі та зберіганні даних. Особливістю даного коду є використання кількох бітів контролю парності. Коди Хеммінга забезпечують виявлення двох помилок і виправлення однієї помилки.

1 Давыдов А.В. Сигналы и линейные системы: Курс лекций.-URL: http://prodav.narod.ru/signals

2. Кузьмин И., Кедрус В.А. Основы теории информации и кодирования. - К.: Вища школа, 1977. - 280 с.

3. Лидовский В.В. Теория информации. - М.: Связь, 2003. - 112 с.

4. Опенгейм А.В., Шафер Р.В. Цифровая обработка сигналов: Пер. с англ. / Под. ред. С.Я. Шаца. -М: Связь, 1979. - 416 с: ил.

5 Филинчук Е.В., Пахомов С.В. Теория информации и помехоустойчивое кодирование: Учебное пособие. – М.: МИФИ, 1989.

6 Шульгин В.И. Основы теории передачи информации. Часть 2. Помехоустойчивое кодирование: Учебное пособие. – Харьков: Нац. аэрокосм. ун-т «Харьк. авиац. ин-т», 2003.

7 Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. М.: Мир,1976, 600 c.

Дата добавления: 2017-01-14