Дифференциальное уравнение свободных колебаний в электрическом колебательном контуре. Формула Томсона

Для возбуждения и поддержания электромагнитных колебаний использует­ся колебательный контур — цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R.

Рассмотрим последовательные стадии колебательного процесса в идеализирован­ном контуре, сопротивление которого пренебрежимо мало (R» 0). Для возбуждения в контуре колебаний конденсатор предварительно заряжают, сообщая его обкладкам заряды ± Q. Тогда в начальный момент времени t= 0 между обкладками конденсатора возникнет электрическое поле, энергия которого Q ² Если замкнуть конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток I. В результате энергия электрического поля будет уменьшаться, а энергия магнитного поля катушки (она равна — воз­растать.

Так как R» 0, то, согласно закону сохранения энергии, полная энергия

Если со­противление R= 0, то свободные электромагнитные колебания в контуре являются гармоническими. Тогда дифференциальное уравнение свободных гармонических колебаний заряда в контуре.

заряд Q совершает гармонические колебания по закону

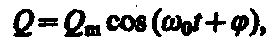(1.1)

где Q _m — амплитуда колебаний заряда конденсатора с циклической частотой w₀, называемой собственной частотой контура, т. е.

(1.2)

и периодом

(1.3)

Формула (1.3) впервые была получена У. Томсоном и называется формулой Томсона.

Дата добавления: 2017-01-14