Оценка центральной тенденции

Частоты

После воздействия

Опытная группа

Классы	8-10
Частоты
			Фон

Классы	5-7
Частоты

(с интервалами в 3 ед.)

Данные, разбитые на классы по непрерывной шкале, нельзя предста­вить графически так, как это сделано выше. Поэтому предпочитают

¹ При большом количестве данных число классов по возможности должно быть где-то в пределах от 10 до 20, с интервалами до 10 и более.

использовать так называемые гистограммы- способ графического представления в виде примыкающих друг к другу прямоугольников:

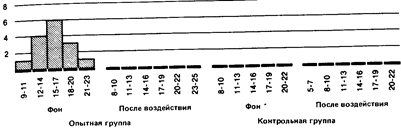
Наконец, для еще более наглядного представления общей конфигу­рации распределения можно строить полигоны распределения частот. Для этого отрезками прямых соединяют центры верхних сторон всех прямоугольников гистограммы, а затем с обеих сторон «замыкают» площадь под кривой, доводя концы полигонов до горизонтальной оси (частота = 0) в точках, соответствующих самым крайним значениям распределения. При этом получают следующую картину:

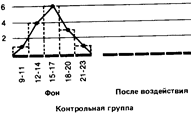
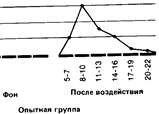
Если сравнить полигоны, например, для фоновых (исходных) значе­ний контрольной группы и значений после воздействия для опытной группы, то можно будет увидеть, что в первом случае полигон почти симметричен (т. е. если сложить полигон вдвое по вертикали, проходя­щей через его середину, то обе половины належатся Друг на друга), тогда как для экспериментальной группы он асимметричен и смещен влево (так что справа у него как бы вытянутый шлейф).

Полигон для фоновых данных контрольной группы сравнительно близок к идеальной кривой, которая могла бы получиться для бесконеч­но большой популяции. Такая кривая-кривая нормального распределе­ния-имеет колоколообразную форму и строго симметрична. Если же количество данных ограничено (как в выборках, используемых для научных исследований), то в лучшем случае получают лишь некоторое приближение (аппроксимацию) к кривой нормального распределения.

Приюжение Б

Если вы построите полигон для фоновых значений опытной группы и значений после воздействия для контрольной группы, то вы наверняка заметите, что так же будет обстоять дело и в этих случаях.

Если распределения для контрольной группы и для фоновых значе­ний в опытной группе более или менее симметричны, то значения, получаемые в опытной группе после воздействия, группируются, как уже говорилось, больше в левой части кривой. Это говорит о том, что после употребления марихуаны выявляется тенденция к ухудшению показате­лей у большого числа испытуемых.

Для того чтобы выразить подобные тенденции количественно, ис­пользуют три вида показателей моду, медиану и среднюю.

1. Мода (Мо)-это самый простой из всех трех показателей. Она соответствует либо наиболее частому значению, либо среднему значе­нию класса с наибольшей частотой. Так, в нашем примере для экспери­ментальной группы мода для фона будет равна 15 (этот результат встречается четыре раза и находится в середине класса 14-15-16). а после воздействия - 9 (середина класса 8-9-10).

Мода используется редко и главным образом для того, чтобы дать общее представление о распределении В некоторых случаях у распреде­ления могут быть две моды; тогда говорят о бимодальном распределе­нии. Такая картина указывает на то, что в данном совокупности имеются две относительно самостоятельные группы (см., например, данные Триона, приведенные в документе 3.5).

Бимодальное распределение

2. Медиана (Me) соответствует центральному значению в последова­тельном ряду всех полученных значений. Так, для фона в эксперимен­тальной группе, где мы имеем ряд

10 11 12 13 14 14 15 15 15 15 17 17 19 20 21,

медиана соответствует 8-му значению, т.е. 15. Для результатов воздей­ствия в экспериментальной группе она равна 10.

В случае если число данных и, четное, медиана равна средней арифметической между значениями, находящимися в ряду на и/2-м и п/2 + 1-м местах. Так, для результатов воздействия для восьми юношей опытной группы медиана располагается между значениями. находящимися на 4-м (8/2 = 4) и 5-м местах в ряду. Если выписать весь

Статистика и обработка дачных 287

ряд для эгих данных, а именно

7 8 9 11 12 13 14 16,

то окажется, что медиана соответствует (11 + 12)/2 = 11,5 (видно.^что медиана не соответствует здесь ни одному из полученных значении).

3 Средняя арифметическая (М) (далее просто «средняя») - это наибо­лее часто используемый показатель центральной тенденции. Ее приме­няют, в частности, в расчетах, необходимых для описания распределения и для его дальнейшего анализа. Ее вычисляют, разделив сумму всех значений данных на число этих данных. Так, для нашей опытной группы она составит 15,2(228/15) для фона и 11,3(169/15) для результатов

воздействия.

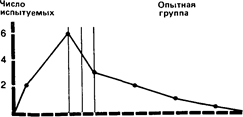
Если теперь отметить все эти три параметра на каждой из кривых для экспериментальной группы, то будет видно, что при нормальном расп­ределении они более или менее совпадают, а при асимметричном

распределении - нет.

Прежде чем идти дальше, полезно будет вычислить все эти показате­ли для обеих распределений контрольной группы-они пригодятся нам в дальнейшем:

9 10 11 12131415161718192021 222324 Фон

Mo=15 Me =15 М=15,2

Дата добавления: 2017-01-14