Терминология деревьев

Деревья

Введение.

НАОБОРОТ

Логопед:

Скажу я слово высоко,

Вы отвечайте низко.

Скажу я слово далеко,

Вы отвечайте близко.

Понятно задание?

Слова для команды «Знайки»:

Молодой – (старый).

Быстрый – (медленный).

Начало – (конец).

Потолок – (пол).

Мокрый – (сухой).

Тихо – (громко).

Белый – (черный).

Широкий – (узкий).

Чистый – (грязный).

Темный – (светлый).

Логопед: А теперь слова для команды «Грамотеи»:

Ночь – (день).

Пустой – (полный).

Хорошо – (плохо).

Твердый – (мягкий).

Трусость – (храбрость).

Богатый – (бедный).

Горячий – (холодный).

Толстый – (тонкий).

Небо – (земля).

Маленький – (большой).

Логопед: Мы просим уважаемое жюри подвести итоги игры и объявить победителя.

Жюри объявляет результаты.

Награждение.

Логопед:

Мы думали и веселились

И даже спорили порой,

Но очень подружились

За нашею игрой,

Игра игрой сменяется,

Кончается игра,

Но дружба не кончается.

Ура! Ура! Ура!

Я решила рассмотреть тему «Бинарные деревья и коды Хаффмана» так как считаю ее наиболее интересной и актуальной. На древовидной структуре основаны многие из наиболее важных алгоритмов. В повседневной жизни мы очень часто встречаем примеры деревьев, и Вы уже наверняка знакомы с этой концепцией. Например, люди часто используют генеалогическое дерево для изображения структуры своего рода; как мы увидим, много терминов, связанных с деревьями, взято именно отсюда. Второй пример - это структура большой организации; использование древообразной структуры для представления ее "иерархической структуры" ныне широко используется во многих компьютерных задачах. Третий пример - это грамматическое дерево; изначально оно служило для грамматического анализа компьютерных программ, а ныне широко используется и для грамматического анализа литературного языка. По моему мнение древовидная структура очень важна не только в компьютерной деятельности, но и даже в повседневной. а Давид Хаффман, предложил очень интересный алгоритм для сжатия данных, который широко используется в наше время. Именно по этому данная тема является актуальной.

Целью моей работы является как можно более близко ознакомится с бинарными деревьями и идеей Давида Хаффмана.

Для достижения цели я поставила следующие задачи:

1. Изучить учебную литературу о структуре и основных операциях бинарных деревьев

2. Рассмотреть практическое применение.

3. Ознакомится с основное идей о кодах Хаффмана.

Реферат состоит из введения, 4 параграфов, рассказывающих о теоретической части вопроса, заключения и списка литературы.

План

1. Древовидные структуры данных. Основные понятия.
2. Бинарные деревья и их описания в программе.
3. Основные операции с деревьями

3.1 Копирование

3.2 Удаление

3.3 Бинарные деревья поиска

1. Вычисление путей и коды Хаффмана.

Массивы и связанные списки определяют коллекции объектов, доступ к которым осуществляется последовательно. Такие структуры данных называют линейными (linear) списками, поскольку они имеют уникальные первый и последний элементы и у каждого внутреннего элемента есть только один наследник. Линейный список является абстракцией, позволяющей манипулировать данными, представляемыми различным образом — массивами, стеками, очередями и связанными списками.

Во многих приложениях обнаруживается нелинейный порядок объектов, где элементы могут иметь нескольких наследников. Например, в фамильном дереве родитель может иметь нескольких потомков (детей). На Рис. 1 показаны три поколения семьи. Такое упорядочение называют иерархическим.

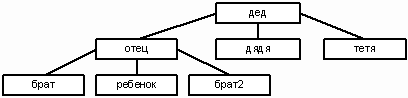
Рис.1.

Мы рассмотрим нелинейную структуру, называемую деревом (tree), которая состоит из узлов и ветвей и имеет направление от корня к внешним узлам, называемым листьями. Эти структуры подобны коммуникационной сети, показанной на Рис. 2, требуют особых алгоритмов и применяются в специальных приложениях.

Рис. 2

Древовидная структура характеризуется множеством узлов (nodes), происходящих от единственного начального узла, называемого корнем (root). На Рис. 3 корнем является узел А. В терминах генеалогического дерева узел можно считать родителем (parent), указывающим на 0, 1 или более узлов, называемых сыновьями (children). Например, узел В является родителем сыновей E и F. Родитель узла H - узел D. Дерево может представлять несколько поколений семьи. Сыновья узла и сыновья их сыновей называются потомками (descendants), а родители и прародители – предками (ancestors) этого узла. Например, узлы E, F, I, J – потомки узла B. Каждый некорневой узел имеет только одного родителя, и каждый родитель имеет 0 или более сыновей. Узел, не имеющий детей (E, G, H, I, J), называется листом (leaf).

Каждый узел дерева является корнем поддерева (subtree), которое определяется данным узлом и всеми потомками этого узла. Узел F есть корень поддерева, содержащего узлы F, I и J. Узел G является корнем поддерева без потомков. Это определение позволяет говорить, что узел A есть корень поддерева, которое само оказывается деревом.

Рис.3.

Переход от родительского узла к дочернему и к другим потомкам осуществляется вдоль пути (path). Например, на Рис. 4 путь от корня A к узлу F проходит от A к B и от B к F. Тот факт, что каждый некорневой узел имеет единственного родителя, гарантирует, что существует единственный путь из любого узла к его потомкам. Длина пути от корня к этому узлу есть уровень узла. Уровень корня равен 0. Каждый сын корня является узлом 1-го уровня, следующее поколение – узлами 2-го уровня и т.д. Например, на Рис. 4 узел F является узлом 2-го уровня с длиной пути 2.

Глубина (depth) дерева есть его максимальный уровень. Понятие глубины также может быть описано в терминах пути. Глубина дерева есть длина самого длинного пути от корня до узла. На Рис. 4 глубина дерева равна 3.

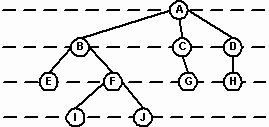
Рис.4. Уровень узла и длина пути

Дата добавления: 2017-01-14