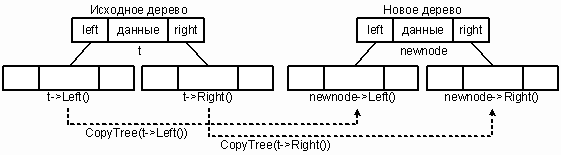
Копирование дерева

Копирование и удаление деревьев

Процедуры копирования и удаления всего дерева вводят новые понятия и подготавливают нас к проектированию класса деревьев, который требует деструктор и конструктор копирования. Функция CopyTree принимает исходное дерево и создает его дубликат. Процедура DeleteTree удаляет каждый узел дерева, включая корень, и высвобождает занимаемую узлами память.

Функция CopyTree использует для посещения узлов обратный метод прохождения. Этот метод гарантирует, что мы спустимся по дереву на максимальную глубину, прежде чем начнем операцию посещения, которая создает узел для нового дерева. Функция CopyTree строит новое дерево снизу вверх. Сначала создаются сыновья, а затем они присоединяются к своим родителям, как только те будут созданы. Этот подход вы должны были использовать в функции MakeCharTree. Например, порядок операций для дерева Tree_0 (Рис. 8) следующий:

d = GetTreeNode('D');

e = GetTreeNode('E');

b = GetTreeNode('B', NULL, d);

c = GetTreeNode('C', e, NULL);

a = GetTreeNode('A', b, c);

root = a;

Сначала мы создаем сына D, который затем присоединяется к своему родителю B при создании узла. Создается узел E и присоединяется к своему родителю C во время рождения (или создания) последнего. Наконец, создается корень и присоединяется к своим сыновьям B и C.

Алгоритм копирования дерева начинает работать с корня и в первую очередь строит левое поддерево узла, а затем - правое его поддерево. Только после этого создается новый узел. Тот же рекурсивный процесс повторяется для каждого узла. Соответственно узлу t исходного дерева создается новый узел с указателями newlptr и newrptr.

При обратном методе прохождения сыновья посещаются перед их родителями. В результате в новом дереве создаются поддеревья, соответствующие t->Left() и t->Right(). Сыновья присоединяются к своим родителям в момент создания последних.

newlptr = CopyTree(t->Left());

newrptr = CopyTree(t->Right());

// создать родителя и присоединить к нему его сыновей

newnode = GetTreeNode(t->data, newlptr, newrptr);

Суть посещения узла t в исходном дереве заключается в создании нового узла на дереве-дубликате.

Проиллюстрируем рекурсивную функцию CopyTree на примере символьного дерева Tree_0. Предположим, что главная процедура определяет корни root1 и root2 и создает дерево Tree_0. Функция CopyTree создает новое дерево с корнем root2. Проследим алгоритм и проиллюстрируем процесс создания пяти узлов на дереве-дубликате.

TreeNode<char> *root1, *root2; // объявить два дерева

MakeCharTree(root1, 0); // root1 указывает на Tree_0

root2 = CopyTree(root1); // создать копию дерева Tree_0

1. Пройти потомков узла A, начиная с левого поддерева (узла B и далее к узлу D, который является правым поддеревом узла B). Создать новый узел с данными, равными D, и левым и правым указателями, равными NULL.

2. Сыновья узла B пройдены. Создать новый узел с данными, равными B, левым указателем, равным NULL, и правым указателем, указывающим на копию узла D.

3. Поскольку левое поддерево узла A пройдено, начать прохождение его правого поддерева и дойти до узла E. Создать новый узел с данными из узла E и полями указателей, равными NULL.

4. После обработки E перейти к его родителю и создать новый узел с данными из C. В поле правого указателя поместить NULL, а левому указателю присвоить ссылку на копию дочернего узла E.

5. Последний шаг выполняется в узле A. Создать новый узел с данными из A и присоединить к нему копии сына B слева и сына C справа. Копирование дерева завершено.

Функция CopyTree возвращает указатель на вновь созданный узел. Это возвращаемое значение используется родителем, когда тот создает свой собственный узел и присоединяет к нему своих сыновей. Функция возвращает корень вызывающей программе.

// создать дубликат дерева t и возвра-тить корень нового дерева

template <class T>

TreeNode<T> *CopyTree(TreeNode<T> *t)

{

// переменная newnode указывает на новый узел, создаваемый

// посредством вызова GetTreeNode и присоединяемый в дальнейшем

// к новому дереву. указатели newlptr и newrptr адресуют сыновей

// нового узла и передаются в качест-ве параметров в GetTreeNode

TreeNode<T> *newlptr, *newrptr, *newnode;

// остановить рекурсивное прохождение при достижении пустого дерева

if (t == NULL)

return NULL;

// CopyTree строит новое дерево в процессе прохождения

// узлов дерева t. в каждом узле это-го дерева функция

// CopyTree проверяет наличие левого сына. если он есть,

// создается его копия. в противном случае возвращается

// NULL. CopyTree создает копию узла с помощью GetTreeNode

// и подвешивает к нему копии сыно-вей.

if (t->Left()!= NULL)

newlptr = CopyTree(t->Left());

else

newlptr = NULL;

if (t->Right()!= NULL)

newrptr = CopyTree(t->Right());

else

newrptr = NULL;

// построить новое дерево снизу вверх, сначала создавая

// двух сыновей, а затем их родителя

newnode = GetTreeNode(t->data, newlptr, newrptr);

// вернуть указатель на вновь создан-ное дерево

return newnode;

}

Дата добавления: 2017-01-14