Бинарные деревья поиска

Удаление дерева

Когда в приложении используется такая динамическая структура, как дерево, ответственность за освобождение занимаемой памяти ложится на программиста. Разработаем функцию DeleteTree, в которой применяется обратный метод прохождения бинарного дерева. Использование обратного метода прохождения гарантирует, что мы посетим всех сыновей родительского узла, прежде чем удалим его. Операция посещения заключается в вызове функции FreeTreeNode, удаляющей узел.

// использовать обратный алгоритм для прохождения узлов дерева

// и удалить каждый узел при его посещении

template <class T>

void DeleteTree(TreeNode<T> *t)

{

if(t!= NULL)

{

DeleteTree(t->Left());

DeleteTree(t->Right());

FreeTreeNode(t);

}

}

Разработаем также функцию ClearTree, которая удаляет все узлы дерева и сбрасывает корень. Функция вызывает DeleteTree для удаления узлов дерева и присваивает указателю на корень значение NULL.

// вызвать функцию DeleteTree для удаления узлов дерева.

// затем сбросить указатель на его корень в NULL

template &lt;class T&gt;

void ClearTree(TreeNode&lt;T&gt; &t)

{

DeleteTree(t);

t = NULL;

// теперь корень пуст

}

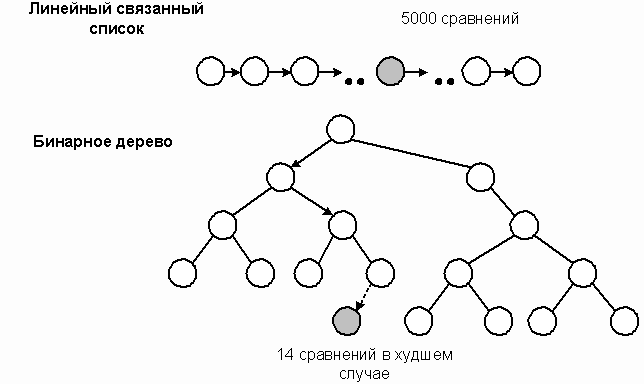
Обычное бинарное дерево может содержать большую коллекцию данных и все же обеспечивать быстрый поиск, добавление или удаление элементов. Одним из наиболее важных приложений деревьев является построение классов коллекций. Для линейных структур сложность алгоритма, реализующего последовательный поиск равна O(N), что неэффективно для больших коллекций. В общем случае древовидные структуры обеспечивают значительно большую производительность, так как путь к любым данным не превышает глубины дерева. Эффективность поиска максимальна при законченном бинарном дереве и составляет O(log₂N). Например, в списке из 10000 элементов предполагаемое число сравнений при последовательном поиске равно 5000. Поиск же на законченном дереве потребовал бы не более 14 сравнений. Бинарное дерево представляет большие потенциальные возможности в качестве структуры хранения списка.

Чтобы запомнить элементы в виде дерева с целью эффективного доступа, мы должны разработать поисковую структуру, которая указывает путь к элементу. Эта структура, называемая бинарным деревом поиска (binary search tree), упорядочивает элементы посредством оператора отношения "<". Чтобы сравнить узлы дерева, мы подразумеваем, что часть или все поле данных определено в качестве ключа и оператор "<" сравнивает ключи, когда добавляет элемент. Бинарное дерево поиска строится по следующему правилу:

Для каждого узла значения данных в левом поддереве меньше, чем в этом узле, а в правом поддереве - больше или равны.

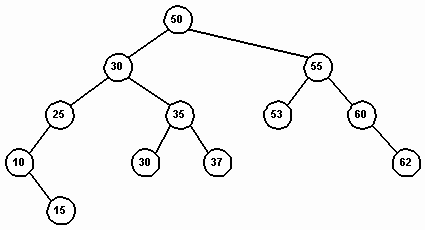
Рис. 9. Бинарное дерево поиска

На Рис. 9 показан пример бинарного поискового дерева. Это дерево называется поисковым потому, что в поисках некоторого элемента (ключа) мы можем идти лишь по совершенно конкретному пути. Начав с корня, мы сканируем левое поддерево, если значение ключа меньше текущего узла. В противном случае сканируется правое поддерево. Такой метод создания дерева позволяет осуществлять поиск элемента по кратчайшему пути от корня. Например, поиск числа 37 требует четырех сравнений, начиная с корня.

Текущий узел	Действие
Корень = 50	Сравнить ключ = 37 и 50
поскольку 37 < 50, перейти в левое поддерево
Узел = 30	Сравнить ключ = 37 и 30
поскольку 37 >= 30, перейти в правое поддерево
Узел = 35	Сравнить ключ = 37 и 35
поскольку 37 >= 35, перейти в правое поддерево
Узел = 37	Сравнить ключ = 37 и 37. Элемент найден.

На Рис. 10 показаны различные бинарные деревья поиска.

Дата добавления: 2017-01-14