Эргодические случайные процессы

Стационарная случайная функция с дискретным спектром частот

Основные сведения из теории

Стационарным в узком смысле называют процесс , если его -мерная плотность вероятности зависит только от величины интервалов , , 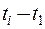и не зависит от положения в области изменения аргумента t.

Стационарным в широком смысле называют процесс , математическое ожидание которого постоянно вдоль всего случайного процесса:

,

а корреляционная функция зависит только от разности . Для стационарного процесса дисперсия

.

Стационарную случайную функцию можно представить в виде разложения

, (13.21)

где ; , – некоррелированные случайные величины. При этом выполняется условие

, . (13.22)

Корреляционная функция будет иметь вид

, . (13.23)

Это уравнение можно переписать в виде

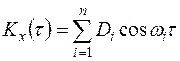, . (13.24)

Отсюда получим величину дисперсии случайного стационарного процесса

. (13.25)

Примем за наименьшую частоту , соответствующую периоду 2Т, а остальные гармонические составляющее будут кратными : ; тогда коэффициенты разложения в (13.24) получают из соотношения

, . (13.26)

Зная , можно реализовать «случайную функцию» с заданной корреляционной функцией на основе разложения (13.21). Величины , задают в виде случайных величин с дисперсией . При этом можно реализовать различные законы распределения при формировании величин , .

Существуют стационарные процессы, которые обладают свойством эргодичности: статистические характеристики, полученные осреднением по времени одной реализации (при достаточно большом интервале наблюдения), совпадают с характеристиками, полученными но множеству реализаций (рис. 13.7, 13.8).

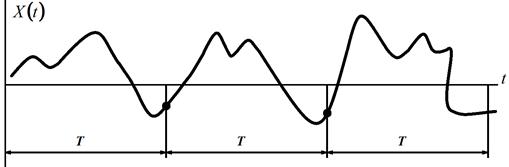
Рис. 13.7. Разбиение стационарного эргодического процесса на «множество» реализаций

Имея таким образом сформированное множество реализаций, можно определить интересующие характеристики эргодического случайного процесса:

– математическое ожидание;

– корреляционную функцию;

– дисперсию случайного процесса;

– спектральную плотность случайного процесса.

Стационарная случайная функция эргодична, если ее корреляционная функция неограниченно убывает по модулю при .

Рис. 13.8. Представление стационарного эргодического процесса
«множеством» реализаций

Следует отметить, что не всякая стационарная случайная функция является эргодичной. Например, случайная функция, каждая реализация которой постоянна по времени, является стационарной, но не эргодической (рис. 13.9).

Рис. 13.9. Графики случайного процесса,
стационарного, но не эргодического

В этом случае математические ожидания, определенные по одной реализации и в результате обработки множества реализаций (рис. 13.9), не совпадают.

Основные статистические характеристики стационарной случайной функции , обладающей эргодическим свойством, определяются следующими выражениями.

; (13.27)

; (13.28)

; (13.29)

. (13.30)

Учитывая, что начало отсчета времени можно переносить, рассмотренные формулы можно переписать в виде

; (13.31)

; (13.32)

; (13.33)

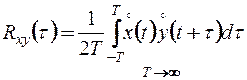; (13.34)

Дата добавления: 2017-01-14