Методические указания. Задачи для практических занятий и самостоятельной работы

Задачи для практических занятий и самостоятельной работы

Определение корреляционной функции из экспериментальных данных

Пусть задана случайная эргодическая функция на интервале наблюдения Т. Разделим промежуток времени Т на N весьма малых интервалов 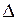так, чтобы функция мало изменялась на протяжении интервала и положим

;

;

;

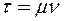Тогда вместо соотношений (13.27)–(13.30) можно записать:

; (13.35)

; (13.36)

; (13.37)

Для обеспечения точности оценок порядка 5 % следует ограничить максимальное значение :

; (13.38)

Если необходимо определить на большом интервале, то необходимо увеличить Т.

Пример 13.1. Случайные функции и заданы своими реализациями (рис. 13.10). Определить взаимную корреляционную функцию , .

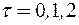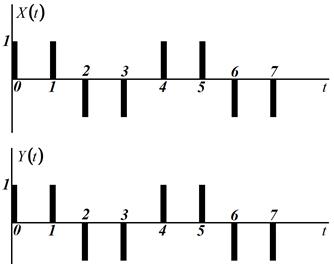
Рис. 13.10. Наблюдаемые случайные сигналы

Решение. По формуле (13.31) при 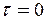получим

При графики функций можно представить в виде графиков, изображенных на рис. 13.11.

Рис. 13.11. Случайные сигналы ,
для расчета корреляционной функции

Тогда

.

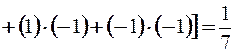Задача 13.1. Случайные процессы заданы графиками , . Определить взаимную корреляционную функцию .

При рассмотрении в задаче 13.1 случая = , что соответствует поиску корреляционной функции , целесообразно использовать аппроксимационный метод на основе приближенного представления корреляционной функции в виде алгебраической суммы экспоненциальных корреляционных функций. В этом случае может быть приближенно представлена в виде такой суммы, что

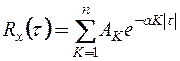; (13.39)

где 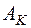– некоторые коэффициенты; 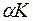– положительные показатели; – число слагаемых.

Для облегчения расчетов по определению корреляционной функции можно из системы экспоненциальных функций , , 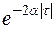, 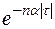построить на основе метода ортогонализации Грамма-Шмидта систему ортогональных нормированных функций , , , 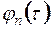. Они имеют следующий вид:

,

,

,

,

.

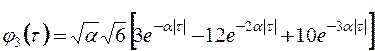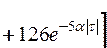При этом разложении представляется в виде

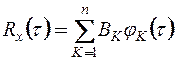, (13.40)

где

. (13.41)

Дата добавления: 2017-01-14