КЭ объемного НДС

КЭ плиты

КЭ плоской задачи теории упругости

Главные напряжения

ПРОВЕРКА ПРОЧНОСТИ ПО РАЗЛИЧНЫМ ТЕОРИЯМ

Вычисление главных и эквивалентных напряжений в стержневых, плоскостных и объемных конечных элементах по усилиям от отдельных загружений, а также по расчетным сочетаниям загружений (РСН) или по РСУ производится при помощи системы ЛИТЕРА.

Главные напряжения вычисляются в соответствии с видом напряженно-деформированного состояния (НДС), полученного в результате расчета схемы. Каждый тип конечных элементов обладает определенными особенностями, соответствующими тому НДС, которое ими моделируется при создании расчетной схемы. Так, например, КЭ балки-стенки моделируют плоское напряженное состояние и т.п.

В общем случае НДС в точке тела описывается шестью осевыми компонентами тензора напряжений:

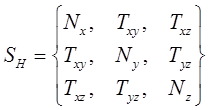(12.1)

Возможны случаи, когда какие-либо напряжения равны нулю. Для плоского НДС, например, тензор напряжений принимает вид:

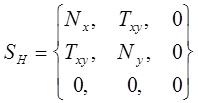(12.2)

В любом случае главные напряжения выстраиваются так: N1³N2³N3.

Моделируется плоское напряженное состояние в плоскости X1OZ1.

Главные напряжения вычисляются в центре тяжести каждого элемента в его срединной поверхности:

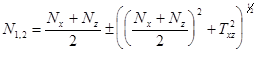(12.3)

Угол наклона наибольшего главного напряжения N1 к оси X1:

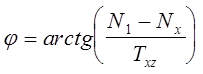(12.4)

Моделируется напряженное состояние в плоскости X1OY1, характеризуемое изгибными усилиями. Осевые напряжения вычисляются для нижней и верхней поверхностей:

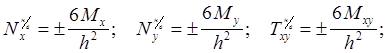(12.5)

h-толщина плиты.

Главные напряжения и углы их наклона вычисляются по формулам (12.3) и (12.4).

В срединной поверхности возникают касательные напряжения:

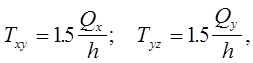(12.6)

которые при вычислении главных напряжений игнорируются.

Определение главных напряжений в этом случае производится из решения кубического уравнения.

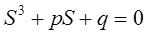(12.7)

где:

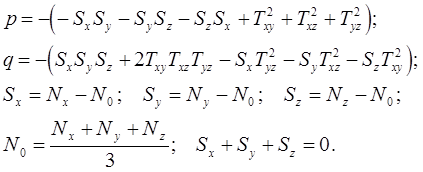
Корни уравнения (12.7):

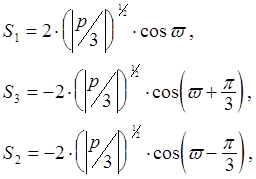(12.8)

где: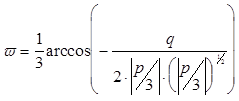

Главные напряжения:

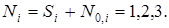(12.9)

Затем вычисляются направляющие косинусы углов наклона осей к осям местной системы координат КЭ из системы уравнений вида:

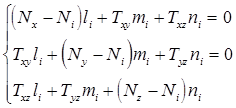(12.10)

где i =1,2,3.

Решив систему трижды, получим матрицу направляющих косинусов:

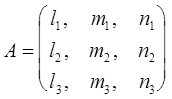(12.11)

В этом случае вычисляются три угла Эйлера, определяющие положение трех главных напряжений относительно местной системы координат (рис. 12.1):

- q (тета)- угол (нутации) между положительными направлениями осей OZ1 и N3 (0 £ q £ p);

- y (пси) - угол (прецессии) между осью OX1 и осью OA (линия пересечения плоскостей X1OY1 и N1ON2), положительное направление которой выбирается так, что OA, OZ1 и N3 образуют правую тройку. Угол y отсчитывается от оси OX1 к OY1 (0 £ y £ 2 p)

- j - (фи) - угол (чистого вращения) между осями N1 и ОA отсчитывается от оси N1 к N2 (0 £ j £ 2 p).

Значения углов Эйлера определяются так:

q = arccos (n₃) (12.12)

При q = 0, j = 0, y = arcsin (m₁),

причем если l₁ < 0, то y = p-arcsin (m₁).

Если y < 0, то y = y +2 p. (12.13)

При q ¹ 0 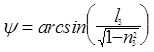, причем если ,

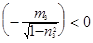то

Если y < 0, то y = y +2 p. (12.14)

Далее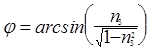

причем если ,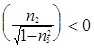

то .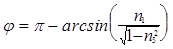

Если j < 0, то j = j +2 p.

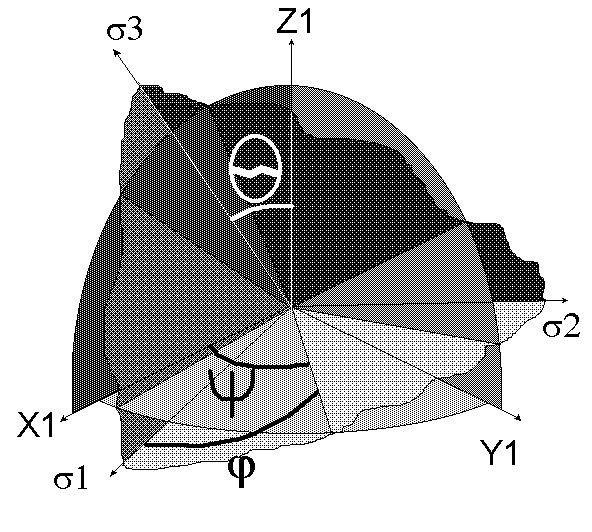
Рис. 12.1

Дата добавления: 2017-01-14