Тема: Исследование концепции системы. Цепи Маркова

Модуль № 2

Граф состояний системы имеет вид, приведенный на рис. 2.17.

Напишите алгебраические уравнения для вероятностей состоя­ний в установившемся режиме. Определите финальные вероятнос­ти состояний системы.

Размеченный граф состояний экономической системы с указанием численных значений интенсивностей перехода системы показан на рис. 2.16.

Вычислите вероятности состояний в стационарном режиме.

Запишите матрицу переходных вероятностей и найдите вероят­ности состояний после двухмесячной эксплуатации.

Неисправны оба узла.

Вероятность выхода из строя (отказов) после месячной эксплу­атации для первого узла - Р_х = 0,4; для второго узла — Р₂ = 0,3, а вероятность совместного выхода их из строя — Р_{х 2} ⁼ 0,1. В исход­ном состоянии оба узла исправны, работают.

Рис. 2.14. Граф состояний

2.12. Размеченный граф состояний системы S имеет вид, пока­
занный на рис. 2.14.

Запишите систему дифференциальных уравнений Колмогорова и начальные условия для решения системы, если известно, что в начальный момент система находится в состоянии S^

2.13. Экономическая система S имеет возможные состояния: S_b S₂, 5₃, 5₄. Размеченный граф состояний системы с указанием численных значений интенсивностей перехода показан на рис. 2.15.

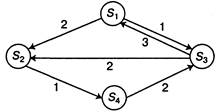
Рис. 2.15. Граф состояний системы

Рис. 2.16. Граф состояний системы

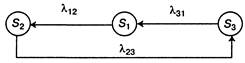
Рис. 2.17. Граф состояний системы

Напишите алгебраические уравнения для вероятностей состо­яний в стационарном режиме и найдите выражение для этих ве­роятностей.

2.16. Найдите вероятности состояний в установившемся режи­ме для процесса гибели и размножения, граф которого представлен на рис. 2.18.

Рис. 2.18. Граф состояний системы

2.17. На автотранспортном предприятии (АТП) эксплуатируют­ся модели автомобилей одной марки. Интенсивность поступления на АТП новых автомобилей А = 5 авт/год. Средний срок службы автомобиля до списания Т_сп = 7 лет. Величина Т_сп распределена —

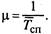
по показательному закону с параметром

Найдите финальные вероятности и математическое ожидание числа эксплуатируемых автомобилей в стационарном режиме, если число автомобилей в АТП не ограничено.

2.18. В задаче 2.17 число эксплуатируемых автомобилей ограни­
чено, п = 60 единиц.

Найдите финальные вероятности и математическое ожидание числа эксплуатируемых автомобилей в стационарном режиме на АТП.

2.19. Найдите вероятности состояний в стационарном режиме
для процесса гибели и размножения, граф которого показан на
рис. 2.19.

Рис. 2.19. Граф состояний системы

2.20. Система учета на предприятии использует компьютерную сеть, в состав которой входит п = 6 персональных компьютеров (ПК). Ежегодно обслуживающий персонал проводит профилакти­ческий осмотр каждого ПК. Суммарный поток моментов оконча­ния профилактических осмотров для всего участвующего персона­ла — пуассоновский с интенсивностью Л = 0,5 ч (число событий в единицу времени). После окончания осмотра с вероятностью Р = 0,86 устанавливается, что ПК — работоспособный. Если ПК

оказался неработоспособным, то вновь проводится профилактика. В начальный момент все ПК компьютерной сети нуждаются в про­филактическом осмотре.

Постройте граф состояний для системы S (6 ПК), напишите дифференциальные уравнения для вероятностей состояний. Най­дите вероятности состояний РДЗ) и математическое ожидание чис­ла персональных компьютеров (М₃), успешно прошедших профи­лактику после трех часов с начала обслуживания (t = 3).

Рис.2.20. Граф состояний системы

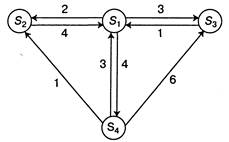
2.23. Граф состояний системы имеет вид, приведенный на рис. 2.21.

2.21. Используйте условие задачи 2.20, за исключением того, что система учета предприятия применяет не шесть, а десять пер­сональных компьютеров.

2.22. Размеченный граф состояний в установившемся режиме для процесса гибели и размножения приведен на рис. 2.20.

Рис. 2.21. Граф состояний системы

Найдите вероятности состояний системы в стационарном режиме.

2.24. Рассматривается производство персональных компьюте­ров на заводе. Поток производимых компьютеров — простейший пуассоновский с интенсивностью 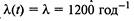(число ком-

пьютеров в год).

Определите вероятность выпуска 5000 компьютеров. За четыре года работы завода вычислите характеристики процесса производ­ства ПК 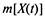ипри 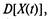/ = 4 года.

Постройте граф состояний процесса производства ПК.

2.25. Аудиторская фирма разрабатывает проекты отдельных до­
кументов для 6 предприятий. Поток разрабатываемых документов —
простейший пуассоновский с интенсивностью 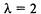месяца"¹. Оп­
ределите закон распределения случайного процесса 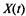— число
разрабатываемых документов на момент времени 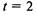месяца, ес­
ли в момент t = О начата разработка документов.

Вычислите математическое ожидание 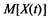случайного про-

цесса X(f), предварительно построив размеченный граф состояний.

2.26. Размеченный граф состояний в установившемся режиме
для процесса гибели и размножения приведен на рис. 2.22.

Рис. 2.22. Граф состояний системы

Найдите вероятности состояний.

2.27. Граф состояний системы имеет вид, приведенный на рис. 2.23.

Рис. 2.23. Граф состояний системы

Найдите вероятности состояний в стационарном режиме. 2.28. Размеченный граф состояний представлен на рис. 2.24. Найдите вероятности состояний 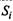и характеристикуна

момент времени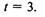

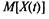
Рис. 2.24. Граф состояний системы

2.29. Размеченный граф состояний представлен на рис. 2.25. Найдите вероятности состояний - 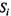и характеристику 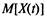на

момент времени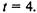

Рис. 2.25. Граф состояний системы

2.30. Размеченный граф состояний представлен на рис. 2.26.

Рис. 2.26. Граф состояний системы

Найдите вероятности состояний 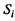и характеристики 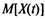и

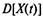для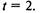

Дата добавления: 2017-01-14