Задачи для самостоятельного решения. Решение типовых задач

Решение типовых задач

Пример 1. Система представляет собой техническое устройство, состоящего из m узлов (m = 3) и время от времени (в моменты 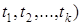подвергается профилактическому осмотру и ремонту. После каждого шага (момент осмотра и ремонта) система может оказаться в одном из следующих состоянии: 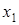– все узлы исправны; 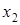– один узел заменен новым, остальные исправны; 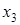– два узла заменены новыми, остальные исправны; 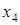– все три узла заменены новыми. Рассматривая состояния системы как марковскую цепь, вычислить вероятности состояний после трех шагов, т.е. 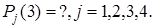В начальный момент времени все узлы исправны. Матрица перехода имеет вид:

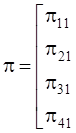
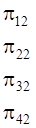
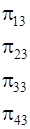
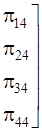
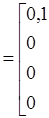
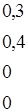
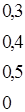
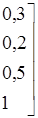
Таким образом:

=?

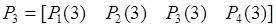Решение. Определим матрицу :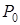

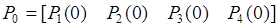
Так как в начальный момент времени система находится в состоянии 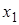, то:

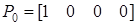
Из (7) имеем:

;

.

;

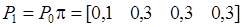
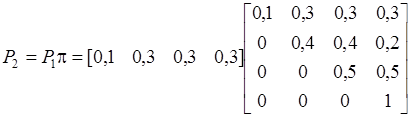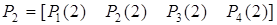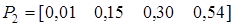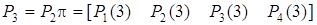
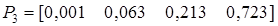
Пример 2. Задана матрица перехо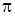да вида:

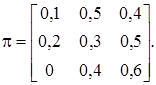
Найти матрицу финальных вероятностей Т вида:

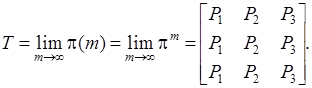
Решение. Из ( 9 ) имеем для n = 3:

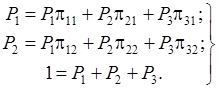
или

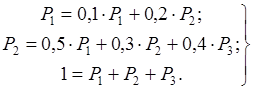( 10 )

Из ( 10 ) имеем:

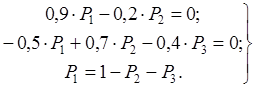( 11 )

Из ( 11 ) имеем:

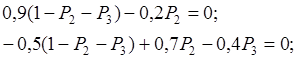
или

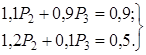( 12 )

Решим систему уравнений ( 12 ), используя правило Крамера. Имеем:

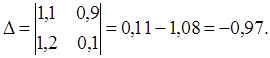
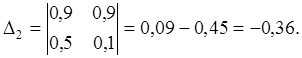
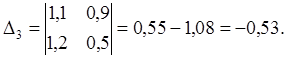
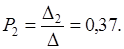
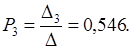
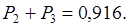
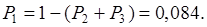
Таким образом:

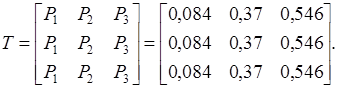
Задача 1. Рассматривается следующий процесс: система представляет собой техническое устройство (ТУ), которая осматривается в определенные моменты времени (скажем, через сутки), и ее состояние регистрируется в отчетной ведомости. Каждый осмотр с регистрацией представляет собой “шаг” процесса. Возможные состояния ТУ следующие: 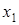– полностью исправно; 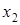– частично неисправно, требует наладки; 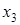– обнаружена серьезная неисправность, требует ремонта; 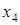– признано непригодным, списано. Матрица перехода:

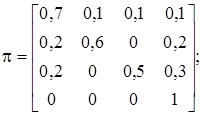
В начальный момент (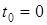) ТУ находится в состоянии 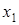(исправно). Найти распределение вероятностей состояний для первых трех шагов ().

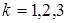Задача 2. Задана матрица перехо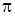да вида:

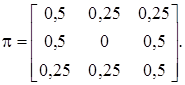
Найти матрицу финальных вероятностей T вида:

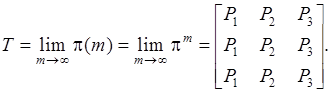
Задача 3. В процессе эксплуатации ЭВМ может рассматриваться как физическая система, которая в результате проверки может оказаться в одном из следующих состояний: 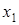– ЭВМ полностью исправна; 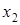– ЭВМ имеет незначительные неисправности в ОП, но может решать задачи; 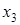– ЭВМ имеет существенные неисправности, может решать ограниченный класс задач; 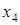– ЭВМ полностью вышла из строя. В начальный момент ЭВМ полностью исправна. Проверка ЭВМ производится в фиксированные моменты времени 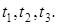Процесс, протекающий в системе, можно рассматривать как цепь Маркова с тремя шагами (1-я, 2-я, 3-я проверки ЭВМ). Матрица перехода:

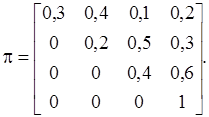
Определить вероятности состояний после трех проверок, т.е.:

=?

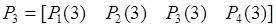Задача 4. Задана матрица перехо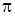да вида:

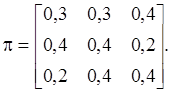
Найти матрицу финальных вероятностей T вида:

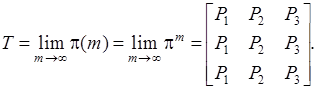
Дата добавления: 2017-01-14