Теоретические сведения. На первом этапе системного анализаанализируется состояние системы в реальных условиях, определяются несоответствия условий существования системы

На первом этапе системного анализаанализируется состояние системы в реальных условиях, определяются несоответствия условий существования системы, выявляются причинно-следственные связи возникновения проблемных ситуаций, определяется степень актуальности проблемы в научном и практическом смысле.

Большое количество различных связей системы с внешней средой представим в виде одной входной и одной выходной связей, выделив их по принципу существенности в заданном отношении. По входным и выходным связям происходит обмен системы со средой путем передачи материальных, энергетических или информационных элементов.

Важной частью анализа проблемной ситуации является определение степени разрешимости проблемы. Необходимо хотя бы приблизительно оценить возможность решения проблемы.

Сложная система управления представляет собой объект дискретной природы, состоящий из большого числа элементов. В ходе исследования имеется возможность, воздействуя на вход системы анализировать ее реакцию на соответствующие входные воздействия.

Состояние системы в каждый момент времени может характеризоваться набором численных значений ее параметров. Эти параметры будем называть фазовыми координатами системы, а состояние системы изображать в виде точки S с этими координатами в некотором условном фазовом пространстве. Тогда изменение состояния системы в процессе ее эволюции соответствует некоторая траектория точки S в фазовом пространстве. Процесс эволюции системы во времени может протекать непрерывно или дискретно. Процесс в системе протекает дискретно, если состояние системы меняется лишь в определенные моменты времени, которые можно пронумеровать.

Описание поведения системы, процесс в которой протекает в дискретном фазовом пространстве, является достаточно сложным. Существует класс случайных процессов, для которых требуемое описание может быть получено более простым путем. Это класс Марковских случайных процессов.

Процесс, протекающий в физической системе, называется Марковским (или процессом без последствий), если для каждого момента времени поведение системы в будущем зависит только от состояния системы в данный момент и не зависит от того, каким образом система пришла в это состояние.

Случайный процесс с дискретным временем будет называться случайной последовательностью или случайной цепью.

Случайная цепь, для которой в каждый момент времени дальнейшая последовательность событий зависит только от состояния системы в данный момент, называется Марковской цепью.

Основной задачей исследования Марковской цепи является нахождение безусловных вероятностей нахождения системы S на любом

(k -м) шаге в состоянии обозначим эту вероятность

( 1 )

где n – число дискретных состояний системы S.

Для нахождения вероятностей необходимо знать условные вероятности перехода системы S на k -м шаге в состояние если известно, что на предыдущем (k – 1)-м шаге она была в состоянии

Обозначим эту вероятность:

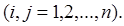( 2 )

Вероятности называются вероятностями перехода цепи Маркова на k -м шаге.

Вероятности перехода можно записать в виде матрицы перехода 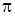размерности

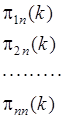
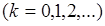( 3 )

Цепь Маркова называется однородной, если не зависят от номера шага Соотношение ( 7.3) примет вид:

( 4 )

Матрица безусловных вероятностей состояний на шаге k определяется соотношением:

( 5 )

Для справедливо соотношение:

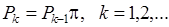( 6 )

Из ( 6 ) имеем:

( 7 )

Матрица финальных вероятностей Т вида:

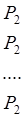
( 8 )

может быть определена путем решения системы алгебраических уравнений:
( 9 )

Здесь – финальные вероятности.

Дата добавления: 2017-01-14