Логистическая кривая.

Уравнение обычного размножения х = кх пригодно, лишь пока число особей не слишком велико. С увеличением числа особей конкуренция из-за пищи приводит к уменьшению скорости прироста. Простейшее предположение состоит в том, что коэффициент k зависит от х как линейная неоднородная функция (при не слишком больших х всякую гладкую функцию можно аппроксимировать линейной неоднородной): k = a - bx.

Мы приходим таким образом к уравнению размножения с учетом конкуренции х = (а — Ьх)х. Коэффициенты а и Ь можно превратить в единицу выбором масштабов t и x. Мы получаем так называемое логистическое уравнение х = (1 — х)х. Векторное поле фазовой скорости v и поле направлений на плоскости (t, х) изображены на рис. 12.

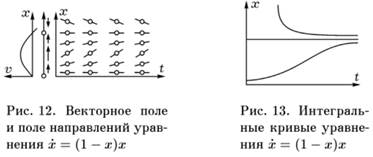
Мы заключаем отсюда, что интегральные кривые выглядят, как изображено на рис. 13. Точнее говоря, мы видим, что:

1) процесс имеет два положения равновесия: х = 0 и х = 1;

2) между точками 0 и 1 поле направлено от 0 к 1, а при х > 1 — к точке 1.

Таким образом, положение равновесия 0 неустойчиво (раз появившееся население начинает расти), а положение равновесия 1 устойчиво (меньшее население растет, а большее — убывает). Каким бы ни было начальное состояние х > 0, с течением времени процесс выходит к устойчивому состоянию равновесия х = 1. Из этих соображений неясно, однако, происходит ли этот выход за конечное или за бесконечное время, т.е. имеют ли интегральные кривые, начавшиеся в области 0 < х < 1, общие точки с прямой х = 1?

Можно показать, что таких общих точек нет и что эти интегральные кривые асимптотически стремятся к прямой х = 1 при t —> +∞ и к прямой х = 0 при t —> —∞. Эти кривые называются логистическими кривыми. Таким образом, логистическая кривая имеет две горизонтальные асимптоты (х = 0 и 1) и описывает переход от одного состояния (0) к другому (1) за бесконечное время.

Задача 1. Найти уравнение логистической кривой.

Решение.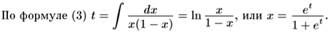

Эта формула доказывает указанное выше асимптотическое свойство логистической кривой.

Дата добавления: 2017-02-01