
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формы представление чисел в ЭВМ для позиционной системы счисления
|
|
|
|
Позиционные системы счисления
1.3.1. Системы счисления позиционные и непозиционные.
Система счисления - совокупность правил записи чисел с помощью определенного набора символов
В зависимости от способа изображения чисел, с/с могут быть позиционные и непозиционные.
В позиционной с/с количественное значение каждой цифры зависит от её местоположения (позиции, разряда) в числе.
Количество цифр, используемых для отображения числа в позиционной системе счисления, называется основанием системы.
Вес разряда - отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде
si = рi,
где i — номер разряда, а р — основание системы счисления.
Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:
| число | . | ||||||
| номера разрядов | -1 | -2 |
Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления
В ЭВМ используются 3 формы записи чисел: естественная, нормальная и нормализованная.
При естественной форме – местоположение запятой, отделяющей целую часть от дробной, строго фиксировано: для правильных дробей – перед старшим разрядом, для целых чисел – после младшего разряда. (25,18 0,526). В современных ЭВМ естественная форма используется в основном для представления целых чисел.
При нормальной форме любое число Х представляется в виде
Х= Рn * |Mx|,
где Р – основание системы счисления
n – целое число (порядок, разряд числа, место запятой)
Mx – мантисса числа (последовательность цифр числа)
Напр. Х = 45,2 м.б. представлено как 4,52*10
452*10-1
При нормализованной форме мантисса лежит в пределах 0 ≤ | Mx| ≤ 1
Напр. Х = 45,2 нормализованная форма 0,452*102
Х = 0,000687 нормализованная форма 0,687*10-3
Запятая фиксируется перед старшим разрядом числа.
В непозиционной с/с цифры не меняют своего количественного значения при изменении их положения в числе. Число отображается равным количеством каких-либо значков.
1.3.2. Двоичная система счисления, как основная для ЭВМ и дополнительные — восьмеричная и шестнадцатеричная системы счисления
В вычислительных машинах при кодировании информации используется двоичная система счисления. Для записи чисел в этой системе используют только две цифры - 0 и 1 (основание системы счисления = 2). Выбор двоичной системы для применения в вычислительной технике объясняется тем, что электронные элементы - триггеры, из которых состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.
Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать.
Для человека самая привычная система счисления – десятеричная, т.е. все числа мы можем описать с помощью 10 цифр, это 0 1 2 3 4 5 6 7 8 9, т.е. основание системы счисления = 10
В программировании часто используется системы счисления, родственные двоичной - восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр.
В восьмеричной (в записи числа присутствуют цифры 0, 1, 2, 3, 4, 5, 6, 7) и
В 16-теричной (в записи числа присутствуют цифры 0 – 9, а дальше используют заглавные латинские буквы А (10), B (11), C (12), D (13), E (14), F (15)).
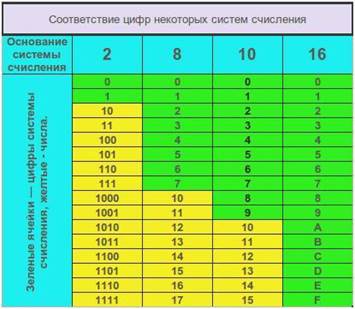
РИС. (1.3)1 Соответствие чисел в двоичной, восьмеричной, десятеричной и шестнадцатеричной системах счисления
Перевод чисел из одной системы счисления в другую, осуществляется по своим правилам.
1.3.3. Правила перевода чисел из десятеричной системы счисления в двоичную, восьмеричную и шестнадцатеричную
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо:
Выполнить последовательное деление с остатком исходного числа и каждого полученного частного на основание новой системы счисления.
Записать вычисленные остатки, начиная с последнего (т.е. в обратном порядке)
Пример

РИС. (1.3)2 Перевод десятичного числа в двоичное
Для перевода правильных дробей из одной системы счисления в любую другую используется метод, базирующийся на умножении переводимой дроби на основание новой системы счисления



1.3.4. Правила перевода чисел из двоичной (восьмеричной и шестнадцатеричной) в десятеричную систему счисления
Обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде:
x = anрn + an-1рn-1 +... + a2р2 + a1р1 + a0р0 + a-1р-1 +...
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Здесь цифры 1, 4, 7 и 6 - это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять (основание системы счисления) возведенную в ту или иную степень. Степень, в которую возводится основание – это разряд цифры за минусом единицы.
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
1. пронумеровать разряды исходного числа;
2. записать сумму, слагаемые которой получаются как произведения очередной цифры на основание системы счисления, возведенное в степень, равную номеру разряда;
3. выполнить вычисления и записать полученный результат (указав основание новой системы счисления — 10).
Примеры

РИС. (1.3)3 Перевод числа из двоичной системы счисления в десятеричную
1.3.5. Правила перевода чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную
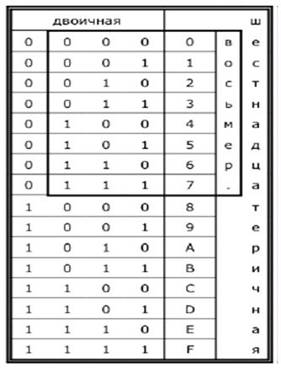
РИС. (1.3)4 Соответствие чисел двоичной системы счисления числам в восьмеричной и шестнадцатеричной системах счисления
При работе с компьютерами широко применяют двоичную систему счисления (поскольку на ней основано представление информации в компьютере), а также восьмеричную и шестнадцатеричную, запись в которых более компактна и удобна для человека. С другой стороны, благодаря тому что 8 и 16 — степени 2, переход между записью в двоичной и одной из этих систем, с кратными основаниями, осуществляется без вычислений.
Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой
Пример. Число 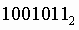 перевести в восьмеричную систему счисления.
перевести в восьмеричную систему счисления.
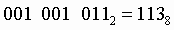
Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой
Пример. Число 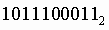 перевести в шестнадцатеричную систему счисления.
перевести в шестнадцатеричную систему счисления.

1.3.6. Правила перевода чисел из восьмеричной и шестнадцатеричной системы счисления в двоичную
Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
Пример. Число 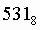 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.
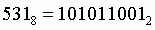
Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
Пример. Число 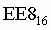 перевести в двоичную систему счисления.
перевести в двоичную систему счисления.

|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 109; Нарушение авторских прав?; Мы поможем в написании вашей работы!