Логические основы ЭВМ

1.4.1. Элементы алгебры логики

Основой построения любого устройства, использующего цифровую информацию, являются элементы двух типов: логические и запоминающие. Логические элементы выполняют простейшие логические операции над цифровыми сигналами. Запоминающие элементы служат для хранения цифровой информации (состояния разрядов кодовой комбинации).
Логическая операция состоит в преобразовании по определенным правилам входных цифровых сигналов в выходные.

Математически цифровые сигналы обозначают поразрядно символами, например x1, x2, x3, x4. Их называют переменными. Каждая переменная может принимать значение "0" или "1". Результат логической операции часто обозначают "0" (ложь) или "1" (истина). Значения логических функций определяются с помощью таблиц истинности.

1.4.2. Логические операции: дизъюнкция, конъюнкция, инверсия, импликация, эквиваленция и их таблицы истинности.

Математическим аппаратом логики является алгебра Буля. В булевой алгебре над переменными "0" или "1" могут выполняться действия:

1. Дизъюнкция (логическое сложение, от лат. disjunctio - разъединение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.

Обозначение: А + В

А ν В

А or B (Паскаль)

A || B (Си)

А	В	А ν В

2. Конъюнкция (логическое умножение, от лат. conjunctio - соединение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.

Обозначение: А * В

А Λ В

А and B (Паскаль)

A && B (Си)

А	В	А Λ В

3. Инверсия (логическое отрицание) делает истинное высказывание ложным и, наоборот, ложное – истинным.

Обозначение:

А	А

4. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.

Обозначение:

А	В	А → В

5. Эквиваленция (равнозначность) – это сложное логическое высказывание, которое определяет результат сравнения двух простых логических выражений и является истинным только при одинаковых значениях истинности простых выражений, входящих в него

Обозначение:

А	В	А ↔ В

6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.

Обозначение:

А	В	А | В

7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.

Обозначение:

А	В	А ↓ В

При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:

1. Инверсия

2. Конъюнкция

3. Дизъюнкция

4. Импликация

5. Эквиваленция

6. Штрих Шеффера

7. Стрелка Пирса

Для последних двух операций приоритет не определен.

Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.

1.4.3. Связь между алгеброй логики и двоичным кодированием.

Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: "1" и "0".

Из этого следует два вывода:
1. одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;

2. на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.

1.4.4. Запись данных и команд в памяти компьютера и регистрах процессора.

Данные и команды представляются в виде двоичных последовательностей различной структуры и длины и заносятся в регистры или ячейки логических устройств (процессор, сопроцессор, оперативная память и др.), которые состоят из логических элементов.

Логическими элементами называются функциональные устройства, с помощью которых реализуются элементарные логические функции.

Логические элементы используются в устройствах цифровой электроники (логических устройствах) для выполнения простого преобразования логических сигналов.

Современные логические элементы выполняются в виде микросхем различной степени сложности. Для этих схем характерно что состояние на входах схем и выходах, определяется только двумя состояниями, к примеру транзистор должна быть либо закрыт, либо насыщен (открыт). В качестве параметра, характеризующего состояние сигнала, обычно выбирают напряжение, уровень которого должен быть ВЫСОКИМ или НИЗКИМ. Состояния высокого и низкого уровня определяют некоторым заданным образом значения булевой алгебры логики. Так для положительной логики принимают состояние ВЫСОКОГО уровня за логическую “ 1” (иногда это логическое значение называют “ИСТИННОЙ”), а состояние НИЗКОГО уровня за логический “ 0” (“ЛОЖЬ”),

например:

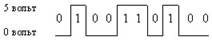
РИС. (1.4)5 Состояние сигнала

1.4.5.Базовые логические элементы, реализующие логические функции в ЭВМ.

Базовые логические элементы реализуют 3 основные логические операции:

· логический элемент " И " - логическое умножение

· логический элемент " ИЛИ " - логическое сложение

· логический элемент " НЕ " - инверсия

Логические элементы компьютера оперируют с сигналами - электрическими импульсами. Есть импульс - логический смысл сигнала - 1. Нет импульса - 0.

На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции. Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности

Логический элемент " И", " ИЛИ "

На входы А и В логического элемента подаются 2 сигнала (00, 01, 10, 11).

На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности

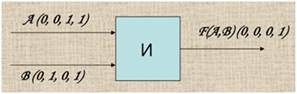
РИС. (1.4)6 Работа конъюнктора

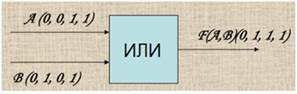
РИС. (1.4)7 Работа дизъюнктора

Логический элемент " НЕ "

На вход логического элемента подается сигнал 0 или 1.

На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии

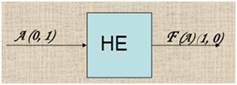
РИС. (1.4)8 Работа инвертора

Логический элемент (логический вентиль) — это электронная схема, выполняющая некоторую простейшую логическую операцию. На рис. приведены примеры условных графических обозначений некоторых логических элементов.

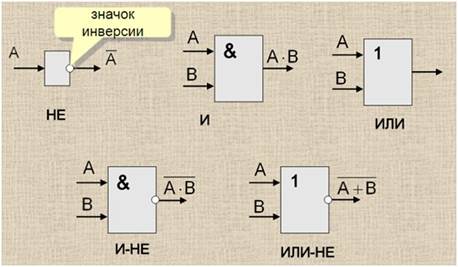
РИС. (1.4)9 Условные графические обозначения основных логических элементов

Логический элемент может быть реализован в виде отдельной интегральной схемы. Часто интегральная схема содержит несколько логических элементов.

Дата добавления: 2017-02-01