
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольные мероприятия и сроки их проведения
|
|
|
|
1. Контрольная работа «Техника дифференцирования».
Срок проведения – 12 неделя
2. ДЗ №3 «Исследование функций и построение графиков»
Срок выдачи 9 неделя, срок сдачи - 16 неделя
3. Контроль по модулю №2 (РК №2) «Исследование функций и построение графиков»
Срок проведения – 17 неделя
Типовые задачи, используемые при формировании вариантов текущего контроля
Домашнее задание №1 «Элементарные функции и их графики»
Задача 1. Найти область определения функции 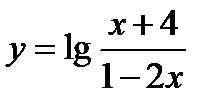 .
.
Задача 2. Исследовать функцию  на четность (нечетность).
на четность (нечетность).
Задача 3. Используя элементарные преобразования, построить эскизы графиков следующих функций:
а)  , б),
, б), 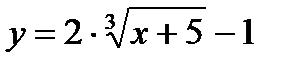 в)
в)  ,
,
г)  , д)
, д)  .
.
Задача 4. Построить эскиз графика рациональной функции 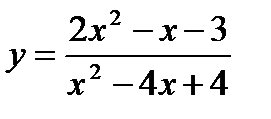 , исследуя его расположение относительно оси абсцисс и асимптот.
, исследуя его расположение относительно оси абсцисс и асимптот.
Задача 5. Используя правила построения графика суммы, произведения, частного или композиции двух функций, построить эскиз графика функции  .
.
Домашнее задание №2 «Пределы и непрерывность»
Задача 1. Для заданной последовательности 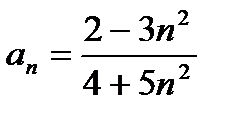 и числа
и числа  доказать, что
доказать, что 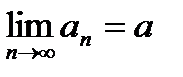 , определив для каждого
, определив для каждого 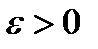 число
число  , такое, что
, такое, что  для всех
для всех  . Заполнить таблицу:
. Заполнить таблицу:
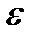
| 0,1 | 0,01 | 0,001 |

|
Задача 2. Вычислить следующие пределы:
а)  ; б)
; б) 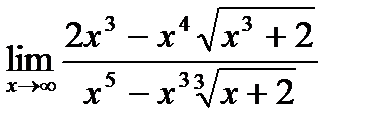 ; в)
; в)  ;
;
г)  ; д)
; д) 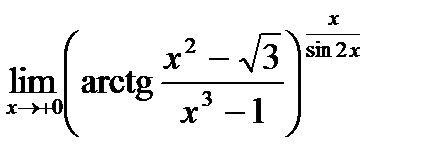 ; е)
; е)  .
.
Задача 3.
1) Показать, что данные функции f и g являются бесконечно малыми или бесконечно большими при указанном стремлении аргумента.
2) Для каждой функции f и g записать главную часть (эквивалентную ей функцию) вида  при
при 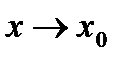 , или
, или  при
при 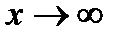 , указать их порядки малости (роста).
, указать их порядки малости (роста).
3) Сравнить f и g при  , если
, если  ,
, 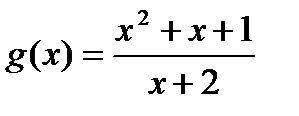 .
.
Задача 4. Найти точки разрыва функции  и определить их характер. Построить фрагменты графика функции в окрестности каждой точки разрыва:
и определить их характер. Построить фрагменты графика функции в окрестности каждой точки разрыва:

Домашнее задание №3 «Исследование функций и построение графиков»
Задача 1. Исследовать заданные функции и построить их графики:
1) 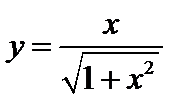 ; 2)
; 2) 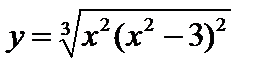 ; 3)
; 3) 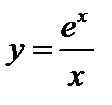 ; 4)
; 4)  .
.
Задача 2. Разложить функцию 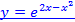 по формуле Маклорена 3-го порядка с остаточным членом в форме Пеано.
по формуле Маклорена 3-го порядка с остаточным членом в форме Пеано.
Задача 3. Из всех равнобедренных треугольников с заданным периметром найти тот, у которого площадь максимальна.
Контрольная работа «Техника дифференцирования»
Задача 1. Для заданных функций найти 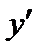 .
.
1.  . 2.
. 2. 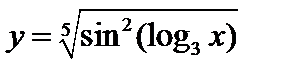 . 3.
. 3. 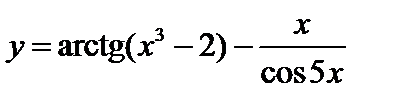 .
.
4. 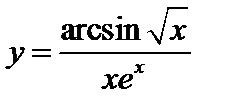 . 5.
. 5. 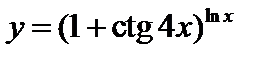 . 6.
. 6. 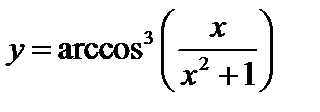
Задача 2. Найти производную 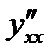 функции
функции 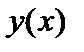 , заданной параметрически:
, заданной параметрически:
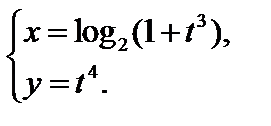
Задача 3. Найти производные 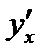 ,
, 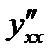 в точке
в точке 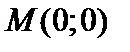 функции
функции  , заданной неявно уравнением
, заданной неявно уравнением  .
.
Задача 4. Составить уравнение касательной и нормали к кривой 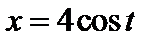 ,
, 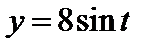 в точке
в точке  . Сделать чертеж.
. Сделать чертеж.
Задача 5. Вывести, исходя из определения, производную функции 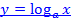 .
.
Замечание: возможно включение теоретических вопросов.
Контроль по модулю №1
Задача 1. Числовая последовательность. Предел последовательности; сходящиеся и расходящиеся последовательности. Доказать теорему о единственности предела сходящейся последовательности.
Задача 2. Сформулировать определение по Коши для предела 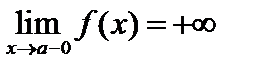 . Привести соответствующий пример (с геометрической иллюстрацией).
. Привести соответствующий пример (с геометрической иллюстрацией).
Задача 3. Вычислить пределы:
1)  , 2)
, 2) 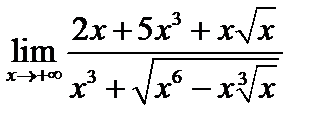 , 3)
, 3) 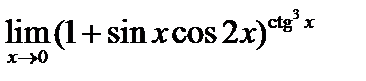 , 4)
, 4) 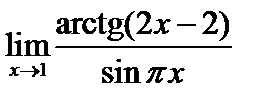 .
.
Задача 4. Выясните, является ли функция 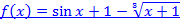 бесконечно малой при
бесконечно малой при 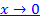 . Если да, найдите значения C и k, для которых
. Если да, найдите значения C и k, для которых 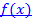 при
при 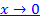 эквивалентна функции
эквивалентна функции 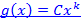 .
.
Задача 5. Найти точки разрыва функции 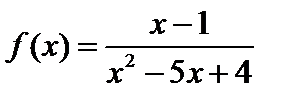 , исследовать их характер, построить график функции в их окрестности.
, исследовать их характер, построить график функции в их окрестности.
Контроль по модулю №2
Задача 1. Сформулировать определение дифференцируемости функции в точке. Доказать теорему о связи дифференцируемости функции с существованием конечной производной.
Задача 2. Исследовать функцию 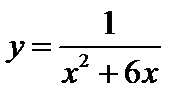 и построить ее график.
и построить ее график.
Задача 3. По графику производной построить график функции (представлен график производной в виде кусочно-линейной функции).
Задача 4. Вычислите предел 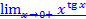 , используя правило Лопиталя-Бернулли.
, используя правило Лопиталя-Бернулли.
Задача 5. Разложите функцию 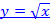 по формуле Тейлора 3-го порядка в окрестности точки
по формуле Тейлора 3-го порядка в окрестности точки 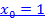 . Записать остаточный член в форме а) Пеано, б) Лагранжа.
. Записать остаточный член в форме а) Пеано, б) Лагранжа.
Задача 6. С помощью формулы Маклорена найти 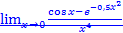 .
.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 69; Нарушение авторских прав?; Мы поможем в написании вашей работы!