Модуль 2 Дифференциальное исчисление функций одного переменного

1. Производная функции в точке. Касательная к графику функции, геометрический смысл производной. Вывод уравнений касательной и нормали к графику функции.

2. Дифференцируемость функции в точке. Теорема о связи дифференцируемости функции с существованием конечной производной (с доказательством). Связь дифференцируемости и непрерывности функции (с доказательством).

3. Основные правила дифференцирования. Вывод формул для вычисления производных суммы, произведения, частного.

4. Теорема о дифференцируемости сложной функции (формулировка).

5. Теорема о дифференцируемости обратной функции (формулировка).

6. Дифференциал функции (определение, геометрический смысл). Инвариантность формы записи дифференциала первого порядка (с доказательством)

7. Формулировки теорем Ферма, Ролля, Лагранжа, Коши.

8. Формулировка теоремы Бернулли – Лопиталя для предела отношения двух бесконечно малых функций.

9. Сравнение на бесконечности порядков роста показательной, степенной и логарифмических функций.

10. Формулы Тейлора с остаточным членом в форме Пеано и в форме Лагранжа (формулировка соответствующих теорем).

11. Формула Маклорена. Разложение по формуле Маклорена основных элементарных функций: , , , , .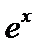

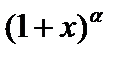12. Необходимое и достаточное условия возрастания и убывания дифференцируемой функции (формулировка).

13. Понятие экстремума. Формулировка необходимого условия существования экстремума дифференцируемой функции. Формулировка достаточного условия существования экстремума функции по ее первой производной. Формулировка достаточного условия существования экстремума функции по ее второй производной.

14. Понятие выпуклой (вверх, вниз) функции (ее графика). Формулировка достаточного условия выпуклости дважды дифференцируемой функции.

15. Определение точек перегиба функции. Формулировка необходимого и достаточного условий для точек перегиба функции.

16. Асимптоты функции. Вывод уравнения наклонной асимптоты.

Дата добавления: 2017-02-01