Вопросы для подготовки к контролю по модулям и к экзамену

Модуль 1. Элементарные функции и пределы

1. Принцип вложенных отрезков (Коши-Кантора).

2. Теорема о существовании точной верхней (нижней) грани ограниченного числового множества.

3. Теорема о единственности предела числовой последовательности.

4. Теорема об ограниченности сходящейся числовой последовательности.

5. Теорема Вейерштрасса о сходимости монотонной ограниченной последовательности.

6. Доказательство сходимости последовательности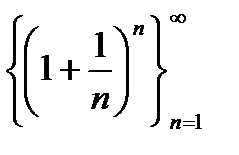

7. Предельная точка числового множества и ее свойства. Лемма о предельной точке (Больцано-Вейерштрасса).

8. Предельная точка числовой последовательности и ее свойства. Критерий сходимости числовой последовательности, связанный с существованием предельной точки.

9. Фундаментальные последовательности и их свойство. Критерий Коши сходимости числовой последовательности.

10. Предел функции. Теорема о связи двустороннего предела с односторонними.

11. Теорема о локальной ограниченности функции, имеющей конченый предел.

12. Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой.

13. Теоремы о сумме бесконечно малых и произведении б.м. на ограниченную функцию.

14. Теорема о пределе суммы, произведения, частного функций.

15. Теорема о пределе сложной функции.

16. Теорема о знакопостоянстве функции, имеющей отличный от нуля предел.

17. Теорема о предельном переходе в неравенстве.

18. Теорема о пределе промежуточной функции (теорема о 2-х милиционерах)

19. Теорема о связи бесконечно малой и бесконечно большой функции.

20. Первый замечательный предел 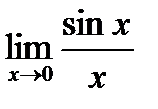и следствия из него.

21. Второй замечательный предел и следствия из него.

22. Теорема Вейерштрасса о пределе монотонной функции.

23. Теоремы об эквивалентных бесконечно малых.

24. Теоремы об эквивалентных бесконечно больших.

25. Непрерывность функции в точке. Свойства функций, непрерывных в точке. Непрерывность сложной функции.

26. Теоремы Больцано-Коши о нуле и о промежуточных значениях непрерывной на отрезке функции.

27. Теоремы Вейерштрасса об ограниченности непрерывной на отрезке функции и достижении этой функцией своих точных верхней и нижней граней.

28. Критерий инъективности непрерывной на отрезке функции. Теорема о точках разрыва монотонной функции.

29. Критерий непрерывности монотонной на отрезке функции. Теорема о непрерывности обратной функции.

30. Равномерная непрерывность. Теорема Кантора о равномерной непрерывности функции, непрерывной на отрезке.

Модуль 2. Дифференциальное исчисление функций одного переменного

1. Понятие производной. Геометрический смысл производной. Связь производной, секущей и касательной к графику функции.

2. Уравнения касательной и нормали к плоской кривой.

3. Дифференцируемость функции. Теорема о связи дифференцируемости функции с существованием конечной производной. Связь дифференцируемости и непрерывности функции.

4. Вычисление производных суммы, произведения и частного двух функций.

5. Теорема о дифференцируемости обратной функции.

6. Теорема о дифференцируемости сложной функции.

7. Вычисление производной функции, заданной параметрически, и заданной неявно.

8. Дифференциал функции. Геометрический смысл дифференциала. Теорема об инвариантности формы записи первого дифференциала.

9. Теорема Ферма. Необходимое условие экстремума дифференцируемой функции.

10. Теорема Ролля. Геометрический смысл теоремы Ролля.

11. Теорема Коши. Теорема Лагранжа. Геометрический смысл теоремы Лагранжа.

12. Теорема Бернулли-Лопиталя для предела отношения бесконечно малых функций.

13. Формула Тейлора с остаточным членом в форме Пеано.

14. Теорема о единственности разложения функции по формуле Тейлора с остаточным членом в форме Пеано.

15. Формула Тейлора с остаточным членом в общем виде, в форме Коши и Лагранжа.

16. Необходимое условие возрастания (убывания) дифференцируемой функции.

17. Достаточное условие возрастания (убывания) дифференцируемой функции.

18. Экстремумы функции. Достаточное условие экстремума по первой производной.

19. Достаточное условие экстремума по второй производной.

20. Достаточное условие экстремума по n -ой производной.

21. Выпуклость функции. Лемма о выпуклости функции.

22. Необходимое и достаточное условие выпуклости функции по первой производной.

23. Достаточное условие строгой выпуклости по второй производной.

24. Связь выпуклости дифференцируемой функции с положением касательной к графику функции.

25. Точки перегиба. Необходимое условие и достаточное условие существования точки перегиба.

26. Необходимое и достаточное условие существования наклонной асимптоты.

Дата добавления: 2017-02-01