Типовые задачи, используемые при формировании

Модуль 2

Контрольные мероприятия и сроки их проведения

Матрицы и системы линейных алгебраических уравнений

Кривые и поверхности 2-го порядка

Упражнения

Занятие 10. Кривые второго порядка.

Ауд.: ОЛ-2 №№ 2.249(а, в), 2.269(а), 2.288(а, в, е) или

ДЛ-2 №№ 471(1,2), 472(1), 541(1), 542(1,2), 597(1), 598(1), 599(1).

Дома: ОЛ-2 №№ 2.249(б), 2.269(б, в), 2.288(б, г, д) или

ДЛ-2 №№ 471(3), 472(2,3), 541(2,3), 542(3), 597(2), 598(2), 599(3).

Занятие 11. Поверхности второго порядка. Исследование методом сечений.

Ауд.: ОЛ-2 №№ 2.393, 2.394, 2.383, 2.379, 2.372, 2.377, 2.405 или МП-6.

Дома: ОЛ-2 №№ 2.395, 2.397, 2.375, 2.382, 2.374, 2.380, 2.381 или МП-6.

Занятие 12. Матрицы. Линейные операции с матрицами. Умножение матриц. Обратная матрица.

Ауд.: ОЛ-2 №№ 3.78, 3.80, 3.81, 3.83, 3.86, 3.90, 3.92, 3.94, 3.103, 3.106, 3.108, 3.112, 3.114, 3.117 или

МП-4 №№ 1.1–1.33 (нечетные); 1.61–1.67 (нечетные).

Дома: ОЛ-2 №№ 3.76, 3.79, 3.82, 3.84, 3.85, 3.91, 3.93, 3.95, 3.104, 3.107, 3.110, 3.113, 3.115, 3.119 или

МП-4 №№ 1.2–1.34 (четные); 1.62–1.68 (четные).

Занятие 13. Решение матричных уравнений. Решение СЛАУ матричным способом. Нахождение ранга матрицы.

Ауд.: ОЛ-2 №№ 3.121, 3.122, 3.125, 3.190, 3.192, 3.198, 3.150, 3.152, 3.154, 3.156, 3.159, 3.166, 3.168 или

МП-4 №№ 1.79–1.97 (нечетные), 1.43–1.49 (нечетные).

Дома: ОЛ-2 №№ 3.123, 3.124, 3.191, 3.199, 3.151, 3.153, 3.157, 3.161, 3.165, 3.167 или

МП-4 №№ 1.80–1.98 (четные), 1.44–1.50 (четные).

Занятие 14. Решение систем линейных однородных уравнений.

Ауд.: ОЛ-2 №№ 3.224, 3.225, 3.228, 3.230, 3.232, 3.235 или

МП-4 №№ 2.1–2.15 (нечетные).

Дома: ОЛ-2 №№ 3.223, 3.226, 3.227, 3.229, 3.231, 3.234 или

МП-4 №№ 2.2–2.16 (четные).

Занятие 15. Решение систем линейных неоднородных уравнений.

Ауд.: ОЛ-2 №№ 3.206, 3.208, 3.210, 3.211, 3.218, 3.220, 3.239 или

МП-4 №№ 2.17–2.33 (нечетные).

Дома: ОЛ-2 №№ 3.207, 3.209, 3.212, 3.213, 3.219, 3.221, 3.236 или

МП-4 №№ 2.18–2.34 (четные).

Занятие 16. Контроль по модулю №2 (РК №2).

.

1. ДЗ №2 «Кривые и поверхности 2-го порядка»

Срок выдачи 6 неделя, срок сдачи - 13 неделя

5. Контрольная работа «Кривые и поверхности 2-го порядка».

Срок проведения – 14 неделя

6. Контроль по модулю №2 (РК №2) «Матрицы и системы линейных алгебраических уравнений»

Срок проведения – 16 неделя

вариантов текущего контроля

1. Домашнее задание №1. «Векторная алгебра и аналитическая геометрия»

Дано: точки , , , 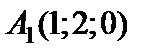; числа , ; угол .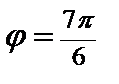

Задание:

Часть 1:

1. Найти длину вектора 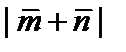, есл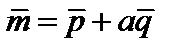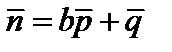и , и 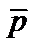, — единичные векторы, угол между которыми равен .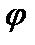

2. Найти координаты точки М, делящей вектор 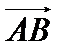в отношении .

3. Проверить, можно ли на векторах 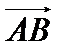и построить параллелограмм. Если да, то найти длины сторон параллелограмма.

4. Найти углы между диагоналями параллелограмма ABCD.

5. Найти площадь параллелограмма ABCD.

6. Убедиться, что на векторах , , 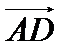можно построить параллелепипед. Найти объем этого параллелепипеда и длину его высоты.

7. Найти координаты вектора 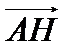, направленного по высоте параллелепипеда 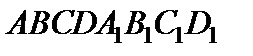, проведенной из точки A к плоскости основания , координаты точки H и координаты единичного вектора, совпадающего по направлению с вектором .

8. Найти разложение вектора 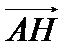по векторам , , .

9. Найти проекцию вектора на вектор .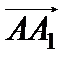

Часть 2:

10. Написать уравнения плоскостей:

а) P, проходящей через точки A, B, D;

б) P₁, проходящей через точку A и прямую A₁B₁;

в) P₂, проходящей через точку A₁ параллельно плоскости P;

г) P₃, содержащей прямые AD и AA₁;

д) P₄, проходящей через точки A и C₁, перпендикулярно плоскости P.

11. Найти расстояние между прямыми, на которых лежат ребра AB и CC₁; написать канонические и параметрические уравнения общего к ним перпендикуляра.

12. Найти точку A₂, симметричную точке A₁ относительно плоскости основания ABCD.

13. Найти угол между прямой, на которой лежит диагональ A₁C, и плоскостью основания ABCD.

14. Найти острый угол между плоскостями ABC₁D (плоскость P) и ABB₁A₁ (плоскость P₁).

2. Домашнее задание №2. «Кривые и поверхности второго порядка»

В задачах 1–2 заданное уравнение линии второго порядка привести к каноническому виду и построить кривую в системе координат OXY.

В задаче 3 по приведенным данным найти уравнение кривой в системе координат OXY.

Для задач 1–3 указать:

1) канонический вид уравнения линии;

2) преобразование параллельного переноса, приводящее к каноническому виду;

3) в случае эллипса: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов; в случае гиперболы: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов, уравнения асимптот; в случае параболы: параметр, вершину, фокус, уравнение директрисы, расстояния от точки C до фокуса и директрисы;

4) для точки C проверить свойство, характеризующее данный тип кривых как геометрическое место точек.

В задаче 4 указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат OXYZ.

1) 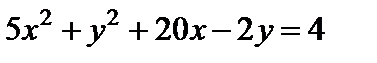, 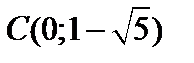; 2) , .

3) Парабола симметрична относительно прямой , имеет фокус 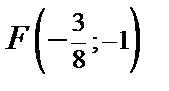, пересекает ось OX в точке , а ее ветви лежат в полуплоскости .

4) .

Контроль по модулю №1 “Векторная алгебра. Аналитическая геометрия”

1. Правые и левые тройки векторов. Определение векторного произведения векторов. Сформулировать свойства векторного произведения векторов. Вывести формулу вычисления векторного произведения двух векторов, заданных своими координатами в ортонормированном базисе.

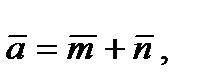
2. Найти угол между векторами если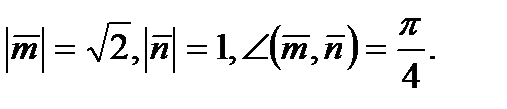

3. Найти, если это возможно, разложение вектора 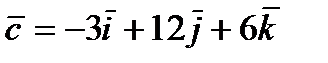по векторам и

4. Составить уравнение плоскости, проходящей через точки 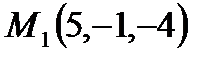, 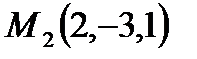и перпендикулярной плоскости 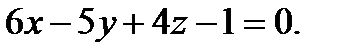Составить канонические уравнения прямой, проходящей через точку 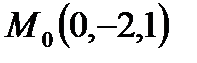и ортогональной к найденной плоскости.

Контрольная работа «Кривые и поверхности второго порядка»

1. Определение эллипса как геометрического места точек. Вывод канонического уравнения эллипса в прямоугольной декартовой системе координат. Основные параметры кривой.

2. Уравнение поверхности привести к каноническому виду. Сделать рисунок в канонической системе координат. Указать название данной поверхности.

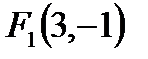3.Составить уравнение равноосной гиперболы, если известны ее центр и один их фокусов . Сделать рисунок.

Контроль по модулю №2 «Кривые и поверхности второго порядка. Матрицы и системы линейных алгебраических уравнений»

1. Однородные системы линейных алгебраических уравнений (СЛАУ). Формы записи однородной СЛАУ. Доказательство критерия существования ненулевых решений однородной СЛАУ.

2.Решить матричное уравнение , где

, .

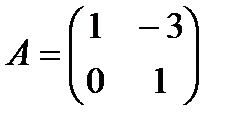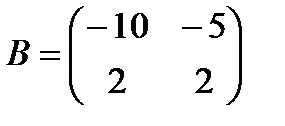Сделать проверку.

3. Вычислить определитель матрицы 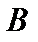. Найти обратную матрицу к .

.

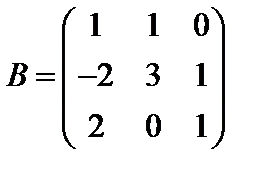4. Решить СЛАУ. Найти нормальную фундаментальную систему решений соответствующей однородной системы, частное решение неоднородной системы; записать через них общее решение данной неоднородной системы:

Дата добавления: 2017-02-01