Решение системы алгебраических уравнений методом Монте-Карло

Пример.

Вычислить интеграл Методом Монте-Карло.

Решение.

Выберем случайный вектор с плотностью распределения , равной = . Для выполняются условия

>0, , .

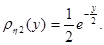Ее можно рассматривать как совместную плотность распределения двух независимых экспоненциально распределенных случайных величин и с плотностями распределения и Тогда

Пусть в результате моделирования независимых компонент случайного вектора получена случайная выборка . Согласно методу Монте-Карло в качестве приближенного значения интеграла следует использовать статистику

Текст программы:

#include <fstream.h>

#include <math.h>

#include <stdlib.h>

#include <limits.h>

#include <time.h>

// basic variate

double bv(double*a, double*b, double*c,int m,int n){

int i, tmp;

double result = c;

for =(i =0;i<n,i ++)

resalt +=b[i]*a[i];

tmp=(int)(resalt/m);

resalt -=((double)tmp)*((double)m);

for(i=1;I<n;i++)

a[i-1]=a[i];

a[n-1]=resalt;

return resalt/m;

}

// exponential variate p(x)=lexp(-lx),x>=0

double ev(double 1,double a) {

return –log(1-a)/1;

}

double avg(double*a,int n){

double s=0;

for(int i=0;i<n;i++)

s+=*(a+i);

return s/n;

}

double var(double*a,int n){

double s=0,s=2;

for(int i=0;i<n;i++){

s+=a[i];

s2+=a[i]*a[i];

}

return(s2-s*s/n)/(n-1);

}

void main() {

int i,j;

const int n=1000;

double a[2][n];//two pseudorandom sequences

double b[2][n];//coefficients

double c[2]; //increment

int m[2] //modules

//initial values

srand((unsigned) time (NULL));

for(j=0;j<2;j++){

m[j] =RAND_MAX-rand();

for(i=0;i<n;i++){

a[j][i]=rand()%m[j];

b[j][i]=rand();

}

c[j]=rand();

}

//computation

double tmp;

double*A =new double[n];

double*x =new double[n];

double*y =new double[n];

ofstream out(“integral.txt”);

for(j=1;j<=5;j++){

for(i=0;i<n;i++){

do{

do{

x[i]=ev(2,dv(a[0],b[0],c[0],m[0],n));

y[i]=ev(0.5,dv(a[1],b[1],c[1],m[1],n));

}while(x[i]-y[i]==0);

tmp= 1+log(pow(y[i]-x[i],2));

}while(tmp<0);

A[i]=sqrt(tmp);

}

out<<avg(A,n)<<”\n”;

out<<var(A,n)<<”\n”;

out<<0.6745*sqrt(var(A,n)/n)<<”\n\n”;

}

}

Некоторые статистические результаты моделирования:

Запустим программу по 5 раз для различных значений n.

№ таблицы	№ эксперимента	n	Ответ	Дисперсия	Вероятная ошибка
			1.48915	0.268116	0.110444
			1.37017	0.446164	0.142472
			1.33855	0.097724	0.0656633
			1.49458	0.13842	0.0793562
			1.45071	0.334751	0.123408
			1.4981	0.322398	0.0856373
			1.21044	0.326385	0.0861652
			1.55455	0.21716	0.070284
			1.3085	0.366371	0.0912909
			1.47881	0.150203	0.0584529
			1.43942	0.268284	0.0494077
			1.47837	0.217818	0.0445189
			1.40335	0.258855	0.045317
			1.43447	0.295186	0.0518256
			1.42966	0.288469	0.0512326
			1.39962	0.219702	0.0316154
			1.43421	0.254309	0.0340144
			1.42465	0.236301	0.032788
			1.38404	0.253826	0.0339821
			1.52162	0.257893	0.0342533
			1.41239	0.272168	0.0157368
			1.42945	0.271058	0.0157046
			1.41602	0.259105	0.0153545
			1.43384	0.243818	0.0148946
			1.40812	0.246367	0.0149723
			1.42914	0.259182	0.00343388
			1.42468	0.260844	0.00344486
			1.42849	0.255745	0.00341103
			1.42793	0.262582	0.00345633
			1.42642	0.257236	0.00342295

Вычислить интеграл аналитически не удается. Полученное с помощью программы Mathematica4.1 точное значение интеграла равно 1.4221. Как видим, полученные в результате выполнения программы значения интеграла близки к точному, однако точность в данном случае невысока. Точность возрастает с увеличением объема выборки. Вероятная ошибка уменьшается.

Моделирование цепей Маркова оказывается естественным образом связанным с решением большого числа задач, и, в первую очередь, с решением систем линейных алгебраических уравнений.

Рассмотрим простейшую вычислительную схему для решения линейных алгебраических уравнений, которая была впервые предложена Дж. Нейманом и С. Уламом [12].

Пусть система алгебраических уравнений задана в виде

(4.3.1)

где 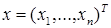– вектор-столбец неизвестных, – вектор правых частей и , – матрица системы.

Предположим, что наибольшее по модулю характеристическое число матрицы А меньше единицы, так что сходиться метод последовательных приближений

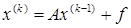, (4.3.2)

Достаточным условием для того, чтобы все характеристические числа матрицы А лежали внутри единичного круга на комплексной плоскости, то есть, чтобы , , 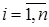может служить неравенство или неравенство .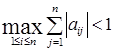

Если положить, что , то

(4.3.3)

– точное решение системы (4.3.1)

Рассмотрим задачу о вычислении скалярного произведения , где h – заданный вектор.

Мы будем связывать с системой (4.3.1) и вектором h некоторую фиксированную цепь Маркова из множества цепей, определяемых парой :

, (4.3.4)

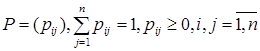, (4.3.5)

для которых выполнены условия:

, если ,

, если 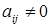; (4.3.6)

Положим

(4.3.7)

Зададимся некоторым целым N, и будем рассматривать траектории цепи Маркова длины N > 0. Объект, переходы которого описываются цепью Маркова, условимся называть частицей и считать, что эта частица изменяет свои состояния (движется в соответствии с траекторией цепи). Движущейся частице приписывается "вес" , который изменяется при движении ее по траектории следующим образом. В начальный момент, когда она находится в состоянии , частица имеет вес ,при переходе из состояния в состояние ее вес становиться равным и т.д., т.е.

. (4.3.8)

Введем случайную величину , определенную на траекториях Марковской цепи длины N

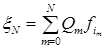, (4.3.9)

Используя формулу умножения вероятностей, найдем

(4.3.10)

Тогда математическое ожидание СВ равно

(4.3.11)

Подставим выражения для , определяемые по формуле (4.3.7), получим

(4.3.12)

Используя определение произведения матриц получим

, (4.3.13)

т.е.

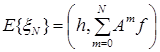. (4.3.14)

Из (4.3.3) и (4.3.14) следует, что при стремиться к .

Итак, доказана следующая теорема.

Теорема 4.3.1. Если все характеристические числа матрицы А по абсолютной величине меньше единицы, то математическое ожидание случайной величины равно

= . (4.3.15)

Для получения приближенного значения – j -й компоненты вектора (решения системы (4.3.1)) выбираем в качестве h единичный вектор , в котором лишь на j -м месте стоит единица. Тогда скалярное произведение (4.3.15) равно . Используя результаты (3) главы, моделируем l реализаций цепи Маркова:

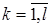, . (4.3.16)

Вы.16заций цепи Маркова:)ие ()чения иницы, то математическое ожидание случайной величинычисляем вдоль цепей (4.3.16) веса согласно формуле (4.3.8), тогда

. (4.3.17)

Приближенное значение для имеет вид

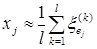. (4.3.18)

Пример.

Решить систему линейных алгебраических уравнений с использованием метода Монте-Карло:

Решение:

Приведем систему к виду, при котором применим метод Монте-Карло:

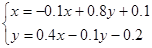
Таким образом, система имеет вид:

Все собственные значения матрицы Ф по модулю меньше 1 и можно применять метод Монте-Карло.

Определим некоторый вектор h следующим образом:

h= для вычисления x, h= для вычисления y.

Моделируем вспомогательную цепь Маркова:

, где .

Вектор вероятностей начальных состояний цепи Маркова: .

Матрица переходных вероятностей имеет вид: .

Каждому состоянию цепи Маркова приписываем веса, которые вычисляются по формулам:

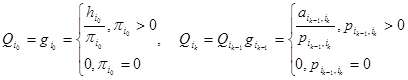
Теперь можем построить СВ 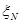по формуле:

,

где - номер реализации цепи Маркова. Тогда приближенное решение вычисляется по формуле:

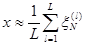или в зависимости от вектора h.

Данный алгоритм реализован на языке С++.

Текст программы:

#include <iostream.h>

#include <stdlib.h>

#include <time.h>

void main(){

int n; //Размерность системы

float x=0,y=0; //Решение системы

float **a; //Исходная матрица

float *f; //Правая часть системы

float *h;

float *pi; //Вектор нач. вероятностей цепи Маркова

float **p; //Матрица переходных состояний цепи Маркова

int N; //Длина цепи Маркова

int *i; //Цепь Маркова

float *Q; //Веса состояний цепи Маркова

float *ksi; //СВ

int m; //Количество реализаций цепи Маркова

float alpha; //БСВ

n=2;

a=new float*[n];

for(int k=0;k<n;k++)

a[k]=new float[n];

f=new float[n];

h=new float[n];

pi=new float[n];

p=new float*[n];

for(k=0;k<n;k++)

p[k]=new float[n];

N=1000;

i=new int[N+1];

Q=new float[N+1];

m=10000;

ksi=new float[m];

for(int j=0;j<m;j++)

ksi[j]=0;

a[0][0]=-0.1; a[0][1]=0.8;

a[1][0]=0.4; a[1][1]=-0.1;

f[0]=0.1;

f[1]=-0.2;

h[1]=1;

h[0]=0;

pi[1]=0.5;

pi[0]=0.5;

p[0][0]=0.5; p[0][1]=0.5;

p[1][0]=0.5; p[1][1]=0.5;

//Моделируем m цепей Маркова длины N

for(j=0;j<m;j++)

{

alpha=rand()/float(RAND_MAX);

if(alpha<pi[0]) i[0]=0; //реализуется 1-е состояние

else i[0]=1; //реализуется 2-е состояние

for(k=1;k<=N;k++)

{

alpha=rand()/float(RAND_MAX);

if(alpha<0.5) i[k]=0;

else i[k]=1;

}

//Вычисляем веса цепи Маркова

if(pi[i[0]]>0) Q[0]=h[i[0]]/pi[i[0]];

else Q[0]=0;

for(k=1;k<=N;k++)

{

if(p[i[k-1]][i[k]]>0)

Q[k]=Q[k-1]*a[i[k-1]][i[k]]/p[i[k-1]][i[k]];

else Q[k]=0;

}

for(k=0;k<=N;k++)

ksi[j]=ksi[j]+Q[k]*f[i[k]];

}

for(k=0;k<m;k++)

x=x+ksi[k];

x=x/m;

cout << x;

}

Результат работы программы:

x=-0.0559199

y=-0.199699

Точное решение системы:

x=-5/89≈0.056179775

y=-18/89≈0.202247191

Дата добавления: 2017-02-01