Составление клауз на основе легенд

Решение

Составление легенд на основе клауз

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

СОСТАВЛЕНИЕ ЛЕГЕНД И КЛАУЗ В ЛОГИКЕ ВЫСКАЗЫВАНИЙ

Лабораторная работа № 7

ЦЕЛЬ РАБОТЫ – приобретение практических навыков по составлению легенд и клауз в логике высказываний.

Основные теоретические сведения, понятия, термины и определения, касающиеся правил составления легенд и клауз, были даны в предыдущей лабораторной работе. Здесь в теоретической части разберем несколько примеров, поясняющих правила составления легенд и клауз.

Пример 7.1. Составить легенду для приведенной ниже клаузы:

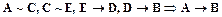
на основе следующих предложений:

А – Падение авторитета власти.

В – Политики, не способные управлять страной.

C – Нарастание анархии в обществе.

D – Высказывание абсурдных идей.

Е – Появление безответственных политиков.

«Падение авторитета власти происходит тогда и только тогда, когда нарастает анархия в обществе (). Нарастание анархии в обществе равносильно появлению на политической арене безответственных политиков ().

Появление подобных политиков приводит к тому, что они высказывают абсурдные идеи (). Высказывание политиками таких идей демонстрирует неспособность их управлять страной (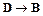). Итак, падение авторитета власти приводит к появлению политиков, не способных управлять страной ()».

(В легенде жирным шрифтом выделены грамматические связки, с помощью которых реализуются логические операции, приведенные в клаузе).

Пример 7.2. Составить легенду для клаузы:

А – Человек занимается спортом.

В – Человек хочет быть здоровым.

C – Наличие высоких спортивных результатов.

D – Одерживание победы на соревнованиях.

Е – Счастливая жизнь.

F – Всеобщее признание.

Один из вариантов легенды.

" Если человек занимается спортом, то он хочет быть здоровым (). Если человек хочет быть здоровым, то у него будет счастливая жизнь (). Кроме того, если человек занимается спортом, то он, как правило, стремится достичь высоких спортивных результатов (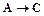). Наличие высоких спортивных результатов (С) позволяет одерживать победы на соревнованиях (D). Если человек одерживает победы на соревнованиях (D), то они влекут за собой всеобщее признание (F). Однако, неверно, что человек хочет жить счастливо и иметь всеобщее признание (). Значит, он не станет заниматься и спортом () ».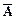

Пример 7.3. Составить легенду для клаузы:

J – Знать язык программирования.

H – Уметь составить рабочую программу.

K – Наличие знакомого программиста.

I – Обучаться в институте.

Один из вариантов легенды.

«Если знать язык программирования (J), то можно составить рабочую программу (H), однако, если есть знакомый программист (K), то можно ее составить с его помощью (H), а если обучаться в институте (I), то будешь знать язык программмирования (J), однако, если умеешь составить рабочую программу (H), то ты должен учиться в институте (I). Но программа не составлена (). Следовательно, ты не знаешь язык программмирования (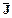) и не имеешь знакомого программиста ().

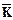Пример 7.4. Пусть имеется легенда для клаузы:

«Все живое способно чувствовать (). Всякое материальное тело занимает определенный объем (). Если нечто занимает пространственный объем и способно чувствовать, то это нечто есть ни что иное, как живой организм (). Пусть существует нечто живое (А), но не являющееся организмом (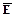). Тогда следует вывод, что это нечто нематериально ()».

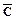Составим предложения для используемых символов клаузы:

А – Быть живым.

В – Способность чувствовать.

C – Материальное тело.

D – Занимать объем.

Е – Быть живым организмом.

На основе полученных выражений составим новый вариант легенды, в котором будем в основном использовать традиционные связки, соответствующие логическим операциям.

«Если нечто является живым (А), то оно способно чувствовать (В) – (). Если существует материальное тело (C), то оно занимает объем (D) – (). Если нечто способно чувствовать (В) и занимает объем (D), то оно является живым организмом (Е) – (). Но если существует нечто живое (А), не являющееся живым организмом (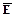), то это нечто нематериальное () – ().

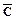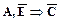Пример 7.5. Пусть имеется следующая легенда.

«Если в одном месте что-то убудет, то в другом месте что-то прибудет – это истина, не требующая доказательства. Но есть такая теория, которая утверждает: где-то в далеком космосе существуют "черные дыры", куда все проваливается, но оттуда ничего не появляется. Эта теория ничего не говорит о существовании "белых дыр", которые действовали бы противоположно "черным". Один иностранный астрономический журнал сообщил координаты "черной дыры". Российский астроном Иванов направил туда свой мощный телескоп и ничего не обнаружил. " Так-так, – сказал Иванов, – но " белую дыру " я все же открою "».

На основе данной легенды выделим предложения и обозначим их символами.

А – Где-то что-то убыло.

В – Где-то что-то прибыло.

C – "Черная дыра" существует.

D – "Белая дыра" существует.

Е – Невозможно ничего увидеть.

Теперь составим клаузу, отвечающую контексту этой легенды, включающую в себя необходимые посылки и два следствия: одно ложное, а другое истинное.

Исходную легенду на основании составленных клауз трансформируем в близкую по смыслу легенду.

«Если в одном месте что-то убудет, то в другом что-то непременно прибудет, и наоборот (A ~ B). Если существует "черная дыра", то в нее все проваливается, то есть в ее окрестностях что-то убывает (). Если существует "белая дыра", то из нее в окружающее пространство должно прибывать вещество (). Если существует "черная дыра", то ее невозможно увидеть, так как она не излучает свет (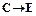). Астроном ничего не увидел (Е). Итак, "белая дыра" существует (D)». Это – ложное заключение.

Истинным заключением является, в частности, следующее: «Итак, если существует "черная дыра", то где-то в пространстве вселенной должно непременно появляться вещество ()».

На основе данной клаузы составим таблицу истинности (табл. 7.1), по которой найдем СДНФ, МДНФ минимальное и все трансверсальные покрытия.

В табл. 7.1 под Р понимается обобщенная причина, то есть конъюнкция всех посылок : .

Клауза считается истинной, если единицы следствия, в данном случае (D) или (), накрывают все единицы обобщенной причины Р, или по-другому единицы обобщенной причины образуют подмножество единиц следствия, или если Р =1, то и следствия или (D)=1 или ()= 1.

Из табл. 7.1 видно, что из пяти единиц обобщенной посылки Р три не покрываютсяединицами ложного следствия (D), что еще раз подтверждает его ложность. Зато единицы истинного следствия () полностью накрывают все пять единиц обобщенной посылки. Для данных единиц составим СДНФ:

Переведя ее в более привычную объектную конъюктивно-дизъюнктивную форму, минимизируем ее и переведем обратно в субъектную конъюктивно-дизъюнктивную форму уже в виде МДНФ

.

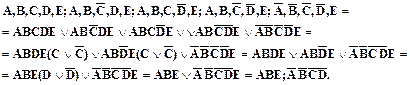
Таблица 7.1

Таблица истинности клауз ,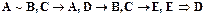

N

A

B

C

D

E

A~B

P

D

Трансверсальные покрытия

.

Минимальное покрытие .

Дата добавления: 2017-02-01