Принцип резолюций

Принцип резолюций – полуконструктивный метод доказательства логических выражений, порождающий конструктивную процедуру и основанный на «склеивании» двух посылочных дизъюнкций, содержащих противоположные переменные в один заключительный дизъюнкт, их не содержащий.

,

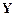где и - произвольные переменные или целые дизъюнкции с любым наборов переменных, включая ноль; и - произвольные термы.

При последовательном применении принципа резолюций происходит уменьшение числа букв, вплоть до их полного исчезновения. При этом исходная клауза конструируется в форме конъюнктивного противоречия.

Докажем с помощью метода резолюций справедливость правила отделения:

или .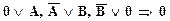

Здесь имеются три дизъюнкции. Склеивая их последовательно, получаем в результате ноль, который говорит о несовместимости заключения и посылок. Это как раз и свидетельствует о справедливости исходной клаузы.

Принцип резолюций целиком заменяет аксиому порядка, поскольку сама эта аксиома может быть доказана в рамках метода резолюций. Действительно,

, , .

Необходимо отметить, что посылка здесь не используется. Это необходимо иметь в виду: необязательно использовать все посылки (их число часто бывает избыточным) – главное получить ноль.

Пусть дана клауза

.

Доказательство ее справедливости следует начать с приведения ее в нормальную конъюктивную форму

.

Выпишем по порядку все посылки и далее начнем их склеивать согласно очередности до тех пор, пока не получим ноль. Справа от каждой новой дизъюнкции или переменных будем писать номера ранее используемых переменных, вошедших в состав уже написанных дизъюнкций.

1.			8.		(2, 4)
2.			9.		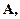(2, 5)
3.			10.		(3, 6)
4.			11.		(3, 8)
5.		(1,3)	12.		(4, 5)
6.		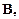(1,4)	13.		(4, 7)
7.		(2,3)	14.		(4, 9)

Подобная стратегия поиска нуля очень непродуктивна. Если же к этой задаче подойти более творчески, то ноль обнаружится на четвертом шаге от начала поиска:

5. 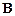(1,4), 6. (2,4), 7. (3,6), 8. 0 (5,7).

В наших расчетах мы пока что использовали форму конъюктивного противоречия. Но исходя из принципа двойственности, метод резолюций можно сформулировать относительно дизъюнктивной тавтологии, при этом принцип резолюций изменится

.

Докажем одну и ту же клаузу двумя способами - в форме противоречия и форме тавтологии. Пусть имеется клауза

.

Доказательство в форме противоречия выглядит так:

.

1 2 3 4

Будем иметь следующие склейки:

5. 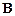(1,2), 6. (1,3), 7. 0 (5,6).

Доказательство в форме тавтологии выглядит аналогично

.

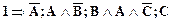1 2 3 4

Склейки: 5. (1,2), 6. 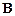(1,3), 7. 0 (5,6).

Метод резолюций удобен для алгоритмизации. Это позволяет использовать его в логических языках программирования и, в частности, в ПРОЛОГе. Алгоритм склеек образует структуру древовидной формы, что хорошо видно на нижеприведенном примере (рис.6.1) для клаузы

Дата добавления: 2017-02-01