При построении доказательств в логике высказываний

Основные понятия и определения, используемые

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ПОСТРОЕНИЕ ДОКАЗАТЕЛЬСТВ В ЛОГИКЕ ВЫСКАЗЫВАНИЙ

Лабораторная работа № 6

ЦЕЛЬ РАБОТЫ – изучение теоретических основ и приобретение практических навыков по построению доказательств в логике высказываний.

Наиболее коротко о логике можно сказать, что логика – это наука о способах доказательства. Выше были рассмотрены логика высказываний и логика Буля. Здесь сначала подчеркнем различие в построении доказательств в этих логиках.

В логике высказываний все доказательства строятся на отношении порядка, то есть на отношении, которое существует между причиной и следствием. Отдельные звенья цепи доказательств в ней связаны символом импликации «».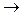

В булевой логике все доказательства строились на отношении эквивалентности. Две логические функции считались эквивалентными, если они принимали одинаковые значения на одинаковых наборах независимых переменных. При использовании формальной записи логических выражений отдельные звенья цепи любого доказательства связывались символом тождественного равенства «» или простого равенства «=». Отношение эквивалентности удовлетворяет законам рефлексивности, симметричности, транзитивности.

Для построения доказательств в алгебре высказываний проведем замену ранее использовавшихся символов логических операций.

Символ импликации «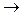» при логическом выводе будем заменять символом «». Вместо символа конъюнкции «», который называется объектным, будем использовать субъектный симво л метаконъюнкции «,» – запятую, вместо объектной дизъюнкции «» - субъектную метадизъюнкцию «;» – точку с запятой, а вместо символа эквиваленции «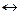» символ эквиваленции – «~».

Тогда утверждение, которое требуется доказать, в логике высказываний оформится в виде следующего причинно-следственного отношения:

, (6.1)

где - посылка (причина), С – заключение (следствие).

Читается: «Если посылки 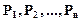истинны, то заключение С тоже истинно» или, по другому: «Если причины имели место, то будет иметь место и следствие С».

Чтобы не спутать объектное высказывание (предложение) с субъектным высказыванием, справедливость которого мы будем доказывать, то предложения вышеприведенного типа будем называть клаузой, от латинского (clause).

Клауза – это записанное с помощью букв и символов операций метапредложение, в котором использовано отношение порядка, оформленное через символ метаимпликации «».

Как и отношение эквивалентности, отношение порядка удовлетворяет трем законам:

рефлексивности – ;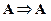

антисимметричности – если , то ;

транзитивности – если и , .

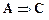Отношение порядка отличается от отношения эквивалентности и предполагает выполнение закона антисимметричности, который можно записать:

если и , то .

Клауза является формальной записью доказываемого предложения. Вместо букв, как и в алгебре логики, можно подставить объектные высказывания, и тогда клауза наполняется конкретным семантическим содержанием, которое называется легендой.

Легенда – это клауза, в которой вместо букв и символов операций используются объектные высказывания.

Дата добавления: 2017-02-01