Аксиоматический метод доказательства логических выражений

Пример 6.1

Имеется клауза 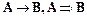, где буквами обозначены следующие высказывания: А – сверкнула молния, В – грянул гром. Необходимо составить легенду.

Решение. «Известно, что если сверкнула молния, то после этого грянет гром. Молния сверкнула. Следовательно, должен и грянуть гром».

Над субъектом, который формулирует метапредложения, может стоять другой субъект, для которого уже предложения первого субъекта окажутся объективными. Тогда клаузу (6.1) второй субъект (метасубъект) запишет для себя следующим логическим выражением, в котором субъектный символ заменен на объектный символ импликации :

.

Это выражение с помощью равносильности второй группы (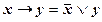) переводим в дизъюнктивную форму

,

в которой группируем члены дизъюнкции в виде и переводим полученное выражение снова в импликацию, в которой посылкой будет первая дизъюнкция в скобках, содержащая переменные с отрицаниями, а следствием дизъюнкция во второй скобке, получим

.

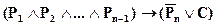На основе полученного выражения клауза (6.1) может быть представлена в другой эквивалентной форме:

. (6.2)

В соответствии с законом коммутативности на месте посылки 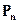в исходном выражении (6.1), может оказаться любая другая или несколько. Тогда, например, клауза

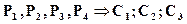
может быть преобразована в другую эквивалентную форму:

. (6.3)

Клауза (6.1), по сравнению с формами (6.2), (6.3), имеет некоторые преимущества и, в частности, используется в языке логического программирования ПРОЛОГ. Ее называют хорновской. Произвольную клаузу всегда можно свести путем эквивалентных преобразований к хорновскому виду.

Если символ метаимпликации «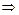» клаузы (6.2) сместить в крайнее левое положение, взяв в качестве посылки единицу, то она превратится в тавтологию, а если его сместить в крайнее правое положение, взяв в качестве следствия ноль, то – в противоречие:

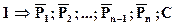– тавтология,

– противоречие.

Порядок преобразования клаузы (6.2) в тавтологию осуществляется следующим образом:

Приведение клаузы (6.2) к противоречию осуществляется аналогично приведенным выше преобразованиям, то есть путем добавления с помощью дизъюнкции нуля, но только не в левую, а в правую часть клаузы (6.2), которая от этого не меняет своего значения.

В полученной тавтологии используется только субъектная метадизъюнкция, а в противоречии – только субъектная метаконъюнкция. В левой части формул вида (6.2) всегда применяется только субъектная метаконъюнкция, а в правой – только субъектная метадизъюнкция.

Далее мы рассмотрим пять методов доказательств справедливости логических клауз: аксиоматический метод, метод таблиц истинности, метод резолюций, метод Вонга и метод натурального исчисления.

Как и в логике Буля, в логике высказываний существует аксиоматический способ доказательств логических выражений.

Аксиоматический метод доказательства логических выражений – метод, при котором из бесконечного числа истинных клауз вычленяется независимая система аксиом, с помощью которой устанавливается справедливость любых других клауз.

Уже упоминалось, что доказательство в логике высказываний строится на отношении порядка, которое является общим случаем для отношения эквивалентности. Поэтому закон симметричности

если 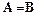, то

всегда можно представить в антисимметричной форме:

если 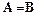, то ,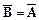

но наоборот нельзя, то есть нельзя записать -если 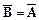, то .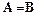

Отсюда следует, что логика высказываний является расширением логики Буля. Поэтому все истинные тождества логики Буля автоматически становятся справедливыми клаузами логики высказываний.

Так, например, в алгебре Буля существует закон склеивания

.

С учетом сказанного его можно представить следующими справедливыми клаузами:

,

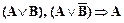перемещая символ метаконъюнкции, получим

, , .

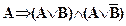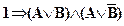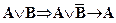Таким образом, независимая система аксиом логики Буля, которая состоит из законов коммутативности, ассоциативности, дистрибутивности, автоматически становится системой аксиом и логики высказываний. А для выражения отношения порядка требуется лишь какое-то одно элементарное высказывание, к которому можно было бы сводить все остальные более сложные высказывания. Введем такое высказывание.

Например,

«Истину может изречь всякий».

Это высказывание можно отобразить клаузой:

.

Она означает, что «если А истинно, то источником этой истинности может быть что угодно, например В». Можно произвести эквивалентное преобразование этой клаузы, например

, (6.4)

тогда ее семантика (значение) тоже изменится, и станет такой: «если ранее было установлено, что А истинно, то истинность В не может проявится так, что А станет ложным» или «истинность одного высказывания (В) не может повлиять на истинность другого высказывания (А)». Путем эквивалентных преобразований, подобных тем, что мы использовали при получении из формулы (6.1) формулу (6.2), клаузу (6.4) всегда можно преобразовать к другим формам, например:

,

,

,

.

,

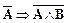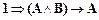В скобках показана процедура преобразования.

Возьмем, однако, в качестве основной аксиомы логики высказываний, выражающей отношение порядка, клаузу (6.4).

Поясним на примере.

Дата добавления: 2017-02-01