КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила вывода
|
|
|
|
Система аксиом исчисления высказываний
Определение доказуемой формулы
Далее для построения исчисления высказываний необходимо выделить класс доказуемых формул.
Для определения доказуемых формул сначала определяются исходные доказуемые формулы (аксиомы), а затем правила вывода, которые позволяют из имеющихся доказуемых формул получить новые доказуемые формулы.
Образование доказуемой формулы из исходных доказуемых формул путем применения правил вывода называется выводом данной формулы из аксиом.
Система аксиом исчисления высказываний состоит из 11 аксиом, которые делятся на четыре группы.
Первая группа аксиом:
I1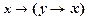 
.
I2 
.
Вторая группа аксиом:
II1 
.
II2 
.
II3 
Третья группа аксиом:
III1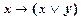 
.
III2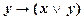 
.
III3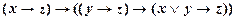 
.
Четвертая группа аксиом:
IV1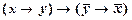 
.
IV 2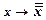 
.
IV 3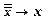 
.
1. Правило подстановки
Если формула А, доказуема на переменных 
, то она будет также доказуема после замены всех входящих в нее переменных на произвольную формулу В.
Операция замены в формуле А переменной формулой В носит название подстановки и символически записывается следующим образом:
.
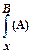Уточним сформулированное правило.
а) Если формула А есть переменная , то подстановка
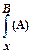дает В.
б) Если формула А есть переменная 
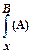, отличная от , то подстановка дает А.
в) Если А – формула, для которой подстановка уже определена, то подстановка В вместо в отрицание А есть отрицание подстановки, то есть подстановка
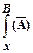дает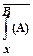 
.
г) Если А1 и А2 – формулы, для которых подстановки уже определены, то подстановка
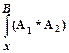дает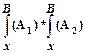 
.
Если А – доказуемая формула, то она будет записываться в виде ├А. В этом случае правило подстановки можно записать схематически следующим образом:
|
├ 
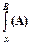
Читается эта запись так: «Если формула А доказуема, то доказуема формула ».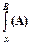
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 98; Нарушение авторских прав?; Мы поможем в написании вашей работы!